Представление периодических несинусоидальных величин рядами Фурье

Определение периодических несинусоидальных токов и напряжений.

Периодическими несинусоидальными токами и напряжени­ями называют токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону.

Они возникают при четырех различных режимах работы элект­рических цепей (и при сочетаниях этих режимов):

1) когда источник ЭДС (источник тока) дает несинусоидальную ЭДС (несинусоидальный ток), а все элементы цепи — резистивные, индуктивные и емкостные — линейны, т. е. от тока не зависят;

2) если источник ЭДС (источник тока) дает синусоидальную ЭДС (синусоидальный ток), но один или несколько элементов цепи нелинейны;

3) когда источник ЭДС (источник тока) дает несинусоидальную ЭДС (несинусоидальный ток), а в состав электрической цепи входят один или несколько нелинейных элементов;

4) если источник ЭДС (тока) дает постоянную или синусоидаль­ную ЭДС (ток), а один или несколько элементов цепи периодически изменяются во времени.

В данной теме рассматриваются методика расчета и особенно­сти работы линейных электрических цепей при воздействии на них несинусоидальных ЭДС и токов — первый из перечисленных режи­мов работы. Второй и частично третий режимы работы обсуждают­ся в других темах.

Представление периодических несинусоидальных величин рядами Фурье.

Из курса математики известно, что любую периодическую функцию f(х) с периодом 2π, удовлетворяющую ус­ловиям Дирихле, можно разложить в ряд Фурье.

Переменная величина х связана со временем t соотношением

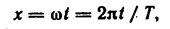
где Т — период функции во времени.

Таким образом, период функции по х равен 2π, а период той же функции по времени равен Т.

Ряд Фурье записывают так:

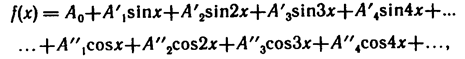
где Аo — постоянная составляющая; А'₁ — амплитуда синусной (изменяющейся по закону синуса) составляющей первой гармоники; A"₁,—амплитуда косинусной составляющей первой гармоники; A'₂ — амплитуда синусной составляющей второй гармоники и т. д.

Здесь

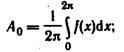
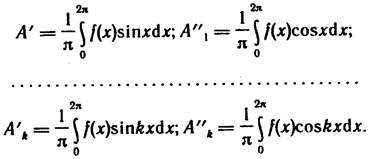
Так как

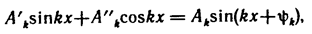
где

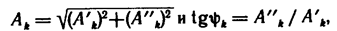
то ряд Фурье (7.1) можно записать в другой форме:

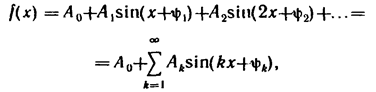
где A_k — амплитуда k-гармоники ряда Фурье.

Гармоники, для которых k — нечетное число, называют нечет­ными; для которых k — четное число, — четными.

Некоторые свойства периодических кривых, обладающих симметрией.

На рис. 1 и 2 изображены три кривые, обладающие некоторыми специфическими свойствами. Кривая рис. 1, а удов­летворяет условию — f(х+π)=f(х).

Рис. 1

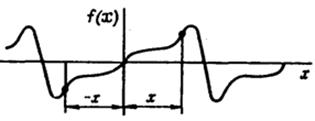
Рис. 2

Кривые, для которых выполнимо это условие, называют симмет­ричными относительно оси абсцисс. Если кривую рис. 1, а сместить по оси х на полпериода и зеркально отразить относительно оси х, то полученная кривая совпадает с кривой f(х).

При разложении таких кривых в ряд Фурье отсутствуют посто­янная составляющая и четные гармоники, т. е. равны нулю коэффи­циенты Ao = А'₂ = А"₂ = А'₄ = А"₄ = ... =0.

Поэтому кривые типа кривой рис. 1,а раскладывают в ряд

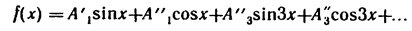
Каждое слагаемое этого ряда удовлетворяет условию —f (x+π) = f (x), например –sin(x+π) = sin x.

Кривая, подобная кривой рис. 1, б, обладает симметрией отно­сительно оси ординат и удовлетворяет условию —f (—х) = f (х).

Если кривую, лежащую левее оси ординат, зеркально отразить относительно оси ординат, то полученная кривая совпадает с кри­вой, лежащей правее оси ординат. При разложении таких кривых в ряд Фурье отсутствуют синусные (А'₁ = А'₂ = А'₃ = ... =0) состав­ляющие, т. е. присутствуют лишь косинусные и постоянная состав­ляющие.

Таким образом, кривые типа кривой рис. 1,б можно разложить в ряд

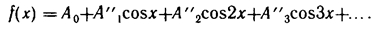
Кривые типа кривой рис. 2 удовлетворяют условию —f (—x) = f (х), их называют кривыми, симметричными относитель­но начала координат. Разложение их в ряд Фурье имеет такой вид:

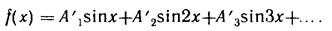
О разложении вряд Фурье кривых геометрически правиль­ной и неправильной форм.

Встречающиеся в электротехнике пери­одические кривые можно подразделить на две группы: 1) кривые геометрически правильной формы, например трапецеидальной, треугольной, прямоугольной и т. п.; разложение их в ряд Фурье дано в справочниках; 2) кривые произвольной (гео­метрически неправильной) формы; чаще всего они заданы в виде графика; разложение их в ряд Фурье производят графически (гра­фоаналитически).