Учет течения при счислении.

Поступательное движение водной массы в морях и океанах называется течением. Элементами течения являются его скорость и направление. Направление течения определяется мнемоническим правилом: «течение идет из компаса». Направление течения показывают в градусах, а иногда в румбах, скорость выражается в узлах.

Под действие упора движителя, судно получает движение относительно воды по направлению диаметральной плоскости (Vл).

Если вода имеет движение относительно Земли, то скорость судна относительно Земли определится геометрической суммой скоростей:

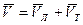
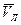И судно будет перемещаться по направлению вектора , если скорость судна и течения 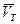постоянны по величине и направлению, суммарная скорость также будет неизменна и судно пойдет по прямой АС.

Угол ПУ между северной частью истинного меридиана и направлением движения судна называется путевым углом (путем), а линия пути АС будет линией пути на течении. Угол b между линиями истинного курса (ИК) и путевым углом (ПУ) называется углом сноса от течения.

Скорость V будет истинной скоростью судна (относительно дна).

ПУ = ИК + (±)b ИК = ПУ – (±)b.

Знаку b зависит от направления сноса. Если течение направлено в левый борт, то знак у b (+), а если в правый борт, то знак-b (-).

Учет течения сводится к решению треугольников (скоростного и путевого). Вначале графически складывают векторы скоростей судна и течения, а затем решают путевой треугольник АВС.

Различают прямую и обратную задачи графического решения треугольника скоростей.

Рис. 1.33Учет течения.

Прямая задача.

В прямой задаче по заданным ИК, Vл, Кт и Vт требуется рассчитать угол b, ПУ и V (Рис.1.33). Для получения линии пути ПУ из точки А проводим линию ИК и на ней от точки А откладываем отрезок, равный вектору скорости судна по лагу (V_Л) в условном масштабе. Обычно берется количество миль в масштабе карты, проходимое судном за час или полчаса. Из конца вектора скорости судна (V_Л) проводим вектор скорости течения (V_Т) в том же масштабе. Соединив точку А с концом вектора скорости течения (Vт), получим линию пути судна (ПУ). Снимаем с карты направление этого пути для сравнения с истинным курсом (ИК) и получения угла сноса от течения (b).

b = ПУ – ИК. (1.43)

Для получения счислимой точки за любой временной промежуток плавания по путевому углу, необходимо по линии истинного курса (ИК) отложить пройденное по лагу расстояние (Sл = РОЛ Кл). Полученную на ИК точку сносим по линии направления течения на линию путевого угла (ПУ) (точки В и С). Надписи на карте производятся над или под линией пути (ПУ) и параллельно ей. Порядок записи таков: пишется ГКК рядом в скобках его поправка, а затем величина сноса от течения со своим знаком (ГКК 69° (-2°) b = +6°).

КК

+(±)d из таблицы девиации

МК

+(±)d с карты

ИК

+(±)b из построения

ПУ_b

Обратная задача

В этой задаче необходимо по заданному ПУ_b, Vл, Кт и Vт рассчитать угол сноса течением (b) и ИК (Рис.1.34).

Задача решается следующим образом:

Пусть на карте проложена линия ПУ (АВ). Из точки А прокладываем вектор скорости течения V_T, выраженный количеством миль. Из конца вектора скорости течения V_T раствором циркуля, равным скорости судна V_Л, делаем на линии ПУ судна засечку (точка Е). Соединив точку Е с концом вектора скорости течения С переносим ее параллельно в начальную точку А, проведя линию истинного курса АD.

Нахождение счислимой точки при уже построенном треугольнике скоростей, производится так же, как и в прямой задаче. По расстоянию Sл находим на линии ИК точку B, и затем через точку B проводим линию, параллельную вектору скорости течения Vт. Пересечение этой линии с линией ПУ и будет счислимым местом судна (точка С) (Рис.1.35).

Кроме графического учета течения существует и аналитический, который применяется при автоматизации судовождения.

Рис. 1.34 Решение обратной задачи.

Рис. 1.35Нахождение счислимой точки.