Основы теории проекции Меркатора

Меркаторская проекция относится к классу цилиндрических, нормальных, равноугольных проекций, в которых картографическая сетка представляет собой взаимно перпендикулярные параллели и меридианы. Расстояние между меридианами соответствует разности долгот. Цилиндрическая проекция задается уравнениями:

x = f(j) и y = c*l,

где х и у - картографические координаты в прямоугольной системе.

Первое уравнение параллелей, а второе меридианов. Термин цилиндрическая говорит о том, что проекция эллипсоида или шара выполняется на поверхность цилиндра. Меркаторская проекция не может быть представлена четкой геометрической картиной из-за налагаемого на нее требования равноугольности.

Этапы проектирования морской навигационной карты:

• Первый этап. Геодезические измерения на поверхности Земли и координатные привязки к референц-эллипсоиду.
• Второй этап. Уменьшение размеров референц-эллипсоида до определенного масштаба с целью развертывания его на плоскость. Это математическое преобразование эллипсоид – глобус сохраняет геометрическое подобие контуров изображений. Масштаб преобразований называется главным масштабом карты (m₀).
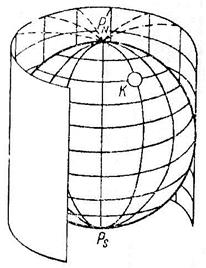• Третий этап. Выбор картографической проекции развертывания глобуса на плоскость и преобразование глобус – карта. При проектировании эллипсоида на плоскость масштаб m₀ будет постоянным на ограниченном множестве точек карты. При удалении этого множества, масштаб изменяется и становится частным (m) другого множества точек. Отношение с = 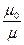называется увеличением масштаба.

Если с = а, где а – радиус экватора, то масштаб вдоль экватора n₀ равен главному масштабу m₀ и в этом случае говорят, что проекция будет на касательный цилиндр. Если масштаб выбран вдоль какой-либо параллели и он равен главному масштабу m₀ , то говорят о проекции на секущий цилиндр.

На рисунке (1.26 а) дана элементарная трапеция поверхности земного эллипсоида в масштабе m₀ и ограниченная отрезками параллелей и меридианов. Локсодромией является диагональ трапеции и имеет элементарную длину ds.

На рисунке 1.26 b) желаемая форма этой трапеции после применения к ней математического преобразования, Рис. 1.25 Построение называемого картографической проекцией.

меркаторской проекции.

а) b)

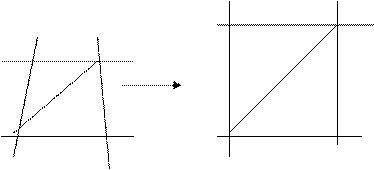
ds dx ds Рис. 1.26

NCosj dl dy = c dl

В этой трапеции масштабы преобразования эллипсоид – глобус по параллели n и меридиану m равны m = n = m₀, откуда углы на глобусе равны углам на эллипсоиде.

При проектировании глобуса на плоскость нужно сохранить равенство углов, при этом изменится конфигурация координатной сетки, но отношение 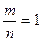остается постоянным.