Осалқылық теориясын қолдану арқылы есепті талдау
Қорларды оңтайлы қолдануға арналған есептің математи-калық моделін қарастырайық.
Мақсат функция:

мына шектеулерде:

Осы есептің қосалқы есебі:
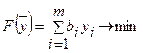
мына шектеулерде:
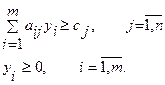
Қосалқылықтың бірінші теоремасы. Егер қосалқы жұп есептердің біреуінің оңтайлы жоспары болса, онда екіншісінің де оңтайлы жоспары болады және мақсат функцияларының мәндері осы оңтайлы жоспарда бір-біріне тең, яғни Zmax = Fmіn.
Егер Z®max (қосалқы есеп үшін F®mіn), ал шектеулердің түрі: “£” (қосалқы есеп үшін “³”) немесе Z®mіn, (қосалқы есеп үшін F®max), ал шектеулер “³” (қосалқы есеп үшін “£” ) түрде жазылады, керісінше жағдайда есептің шешімі жоқ.
Қосалқылықтың 2-ші теоремасы. Тек мына қатынастар орын-далғанда:
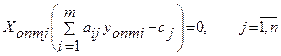

бастапқы есептің жоспары 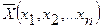 және қосалқы есептің жоспары
және қосалқы есептің жоспары 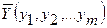 оңтайлы делінеді.
оңтайлы делінеді.
Осы көрсетілген жағдай, бір-бірімен қосалқыланған екі есептің біреуінің оңтайлы шешімі бойынша екіншісін анықтайды.
2-ші теореманың маңызы: егер қосалқы бағалар уі>0, онда қорлар жетімсіз (яғни олар толығымен қолданылған, ал олардың қолданбаған мөлшерлері Si=0). Егер уі=0, онда і-қор мөлшері артық, сондықтан Si>0. Егер уі<0, онда оңтайлы мәні ізделініп отырған і-айнымалының мәні ең шеткі төменгі шегіне тең, оның бір бірлікке өсуі мақсат функция мәнін қосалқы бағаның мәніне кемітеді.
Қосалқылықтың 3-теоремасы. Қосалқы есептің оңтайлы шешіміндегі yі-ң мәні, бастапқы есептің шектеулерінің бос мүше-лерінің (bі) мақсат функцияға әсерлігінің бағалары, яғни егер bі®Dbі бірлікке өзгерсе, мақсат функция (DZ) қаншаға өзгеретінін көрсетеді немесе математикалық түрде:
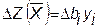 ,
,
мұндағы yі – bі-ң қосалқы бағасы (тәжірибеде өте маңызды көрсеткіш. Оны өндірістік қордың жалпылама объективті бағасы немесе көлеңкелік құны немесе құндылығы деп атайды).
Қосалқылықтың 3-теоремасынан:
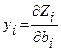 ,
,
мұндағы 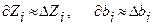 онда
онда 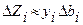 . Осы теңдіктен, егер есеп қорларды оңтайлы қолдануға бағытталған болса, онда і-қордың мөлшерінің өзгеруі мақсат функция мәнінің сызықты байланыста өзгеруін көрсететінін байқауға болады.
. Осы теңдіктен, егер есеп қорларды оңтайлы қолдануға бағытталған болса, онда і-қордың мөлшерінің өзгеруі мақсат функция мәнінің сызықты байланыста өзгеруін көрсететінін байқауға болады.
Егер yі-мәні аз мөлшерде болса, онда і-қор мөлшерінің шама-лы өзгеруіне оңтайлы табыс мәнінің аздап қана өсуі сәйкес келеді, яғни і-қордың құндылығы онша көп емес.
Егер yі = 0, онда і-қор мөлшері көбейсе де оңтайлы табыс мәні өзгермейді, себебі осы қордың өндірістегі құндылығы нөлге тең, яғни қор құнсыз. Шындығында да, егер шикізаттың (қордың) мөлшері өзіне қажеттілік мөлшерден көп болса, онда оның қажет-тіліктен қалған бөлімі өндіріске керек емес, яғни ол құнсызданады және оны нөлге теңестіреді.
Егер yі- мәні көзге түсетіндей жоғары болса, онда і-қоры мөлшерінің шамалы өзгерісі оңтайлы табыс мәніне көп өзгерістер тудырады, яғни і-қорының өндірісте құндылығы жоғарлайды. Осы қор мөлшерінің азайуы өндірілетін өнім көлемін көп төмендетеді.
Сонымен, уі-айнымалысы і-қорының құндылығының сипат-тамасы деп есептелінеді. Мысалға, і-қор мөлшері бір бірлікке өссе (Dbі=1) оңтайлы табыс мәні yі- бірлігіне өседі. Сондықтан yі-ді қордың «Шартты құны», і-қоры бірлігінің бағасы, жалпылама объективті баға ретінде қарастырады.
Қосалқы баға yі-оңтайлы табыстың і-қоры бойынша жекелен-ген туындысы, сондықтан ол, і-қор мөлшері өзгеруіне байланысты оңтайлы табыс мәнінің өзгеру жылдамдығын сипаттайды. Сонымен қатар, yі-бойынша мақсат функцияның мәніне шектеулер қандай дәрежеде әсер ете алатынын анықтауға болады.
Қорлар мәнінің қандай өзгеру аралықтарында олардың құн-дылығы (уі) өзгерізсіз қалатынын мына формулалармен анық-тайды:

мұндағы хj–оңтайлы шешімдегі айнымалылардың мәні;
dіj=A-1, оңтайлы шешімдегі A=(aіj)m´n базисіне кері
матрица.
Егер жоспарға жаңа өнімдердің түрлері енгізілсе, онда олар-дың бағасы мына формула арқылы табылады:
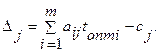
Егер 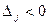 болса, онда жаңа өнім жоспарды жақсартады, ал
болса, онда жаңа өнім жоспарды жақсартады, ал 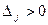 болған жағдайда жаңа өнімді жоспарға енгізудің қажеті жоқ.
болған жағдайда жаңа өнімді жоспарға енгізудің қажеті жоқ.
Қосалқы есептің экономикалық талдау әдістерін тәжірибелік есептің шешімі бойынша қарастырайық.
Мысал: Фирма 4 түрлі (А, Б, В, Г) шикізаттан (олардың мөлшері: 18; 16; 8 және 6 тонна) үш түрлі бұйымдар шығарады. Әр- түрлі бұйымдар үшін әрбір шикізаттың шығыны мынадай: 1-ші бұйымның бір бірлігіне: А®1, Б®2, В®1, Г®0 тонна, сәйкесін-ше, 2-бұйымның бір бірлігіне: 2; 1; 1; 1 және 3-бұйымның бір бірлігіне: 1; 1; 0; 1. Әрбір бұйымның бір бірлігінен түсетін пайда 1-шіден –3 ақша бірлігі (а.б.), 2-ден – 4 а.б. және 3-ден – 2 а.б.
Табу керек:
– максимальды пайда келтіретін үш түрлі бұйымдарды өндіру жоспарын;
– әрбір шикізаттың қажеттілік құнын;
– шикізаттар өзгерісі (мысалға, А– 6 тоннаға көбейсе, Б–3 тоннаға кемісе, В–2 тоннаға және Г–2 тоннаға көбейсе) максимальды пайдаға қалай әсер ететінін, сонымен қатар әрбір шикізаттың өзгерісі және барлығының бірдей өзгерісі пайдаға қалай әсер етеді;
– фирмаға 4-ші жаңа бұйым өндірумен айналысу пайдалы ма? Бұл бұйымның бір бірлігіне шикізаттардың шығыны жоғарыда көрсетілген реттеріне сәйкес мынадай: 1; 2; 2 ; 0 а.б., ал оның бір данасынан алынатын пайда 15 а.б.
Шешімі: 1. Бұйымдарды оңтайлы өндіру жоспарын мына түрде:  (х1, х2, х3) белгілеп, есептің математикалық моделін жазайық. Максимальды пайдаға жету көзделінетін есептің мақсат функциясы:
(х1, х2, х3) белгілеп, есептің математикалық моделін жазайық. Максимальды пайдаға жету көзделінетін есептің мақсат функциясы:
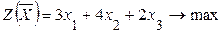
мына шектеулерде:
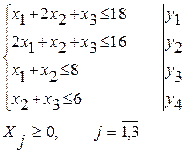
Модельде шектеулер жүйесінің әрбір yi – і-теңсіздіктің қосалқы бағасы. Қосалқы есептің моделін құрайық.
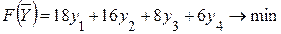

Егер есепті компьютер көмегінсіз симплекс әдісімен қолмен шығаратын болсақ, онда мақсат функцияларды мына түрде жазып:
– тура есеп
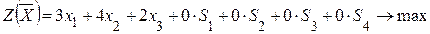
– қосалқы есеп
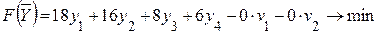
шектеулерді теңдікке түрлендіреміз:
Тура есеп (ТЕ)Қосалқы есеп (ҚЕ)
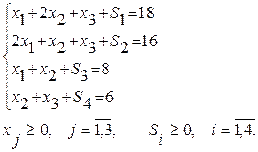
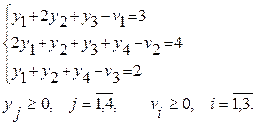
Көріп отырмыз, модельге қосымша (Si –тура есепке және vi- қосалқы есепке) айнымалылары енгізілген, нәтижесінде шектеулер жүйесі теңсіздітерден теңдік түріне ауыстырылған. Қосымша айнымалылар Si шамалары аталған шикізаттардың қолданылмаған мөлшерлерін көрсететінін, ал қосымша қосалқы айнымалылар vi шамалары, оған сәйкес негізгі айнымалының мәні бір бірлікке өзгергенде мақсат фукция мәні осы шамаға өзгеретінін, атап өтейік.
Қосалқылықтың 1-теоремасы бойынша қарастырылып отыр-ған екі есептің біреуінің шешімін анықтасақ екіншісінің де шешімі табылады.
Бірінші тура есепті симплекс әдісімен шығарғанда ақырғы симплекс кесте мынадай болды:
1.4- кесте
| cj | БП | x1 | x2 | x3 | S1 | S2 | S3 | S4 | bi |
| S1 | – 1 | – 1 | |||||||
| x3 | 0,5 | – 1 | 0,5 | ||||||
| x1 | 0,5 | – 0,5 | |||||||
| x2 | – 0,5 | 0,5 | |||||||
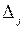
| 0,5 | 1,5 |
Екі есептің бір-бірімен байланыстарын көрнекі көрсету үшін шешім нәтижелерін бір кестеге жинайық (1.5-кесте).
1.5-кесте
| Айнымалылар | Айнымалылар | ||
| ТЕ негізгі | ҚЕ қосымша | ТЕ қосымша | ҚЕ негізгі |
| x1=5 | v1=0 | S1=4 | y1=0 |
| x2=3 | v2=0 | S2=0 | y2=0,5 |
| x3=3 | v3=0 | S3=0 | y3=2 |
| S4=0 | y4=1,5 |
1.4-кестеден 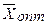 (5; 3; 3; 4; 0; 0; 0), мақсат функция
(5; 3; 3; 4; 0; 0; 0), мақсат функция 
Қосалқылық теоремасы бойынша: 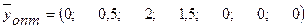 , мақсат функция
, мақсат функция 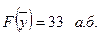
Екінші теорема. y1= 0 → S1= 4 → Ашикізатыартығымен.
y2=0,5, y3=2 және y4=1,5 → S2=0, S3=0 және S4=0 → Б, Вжәне Гшикізаттары жетіспейді.
В заты шикізаттардың ішіндегі ең құндысы, оның қосалқы бағасы y3=2, онан кейін құндылығы жоғары Г заты (y4=1,5). Құндылығы азы Бзаты, оның қосалқы бағасы у2 = 0,5. Ең құнсызы Азаты, оның қосалқы бағасы y1=0.Сөйтіп, қарастырылып отырған есеп үшін, шамасы ең көп жетіспейтін зат құнды болып есептелін-се, ал шамасы артығымен зат құнсыз болып есептелінеді.
Үшінші теорема. Ең құнды В шикі затын қарастырайық. Фирмадағы осы шикі заттың шамасын бір бірлікке өзгертейік, яғни  және в3 = 8+1= 9.
және в3 = 8+1= 9.
Онда 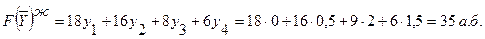 , яғни
, яғни 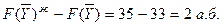 – бұл В шикізатының қосалқы бағасы y3 =2.
– бұл В шикізатының қосалқы бағасы y3 =2.
Шикізаттар қоры бағаларының тұрақтылық аралығын анық-тау үшін, оңтайлы шешімдегі шектеулер жүйесінің базистік айны-малылар коэффициенттері матрицаларының кері матрицасын табамыз. Оңтайлы шешімдегі базистік айнымалылар: х1, х2, х3 және S1. Осы айнымалылардың шектеулер жүйесіндегі коэффициент-терінің матрицасы мынадай түрде (модельді қараңыз):
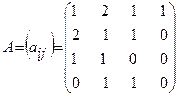
жазылады.
Онда А-матрицаның кері матрицасы мынадай болады (кестені қараңыз):
 .
.
Бағалардың тұрақтылық аралығын шикізаттардың әрбір түріне іздейік:

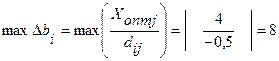 .
.
Бірінші шектеуге байланысты 1-ші шикізаттың бағасының тұрақтылық аралығы:
 .
.
Осы сияқты, басқа шектеулерге сәйкес қалған шикізаттар үшін бағаның тұрақтылық аралығын анықтаймыз:

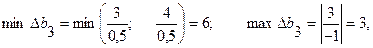
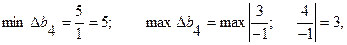
Екінші шектеуге сәйкес 2-ші шикізаттың қосалқы бағасының тұрақтылық аралығы:
(16 – 3; 16 + 6) = (13; 22),
Үшінші шектеуге сәйкес 3-ші шикізаттың:
(8 – 6; 8 + 3) = (2; 11),
Төртінші шектеуге сәйкес 4-ші шикізаттың:
(6 – 5; 6 + 3) = (1; 9).
Есептің шарты бойынша шикізаттардың +6; -3; +2 және +2 тоннаға өзгерісі, сәйкес қорларды мынадай шамаға жеткізеді: 24; 13; 10; 8 т. Қорлардың бұл шамалары қосалқы бағалардың тұрақтылық аралықтарында жатуына байланысты (шикізаттардың тұрақтылық аралықтарын қараңыз), олардың пайдаға жеке-жеке әсерлері мына формула арқылы анықталынады:
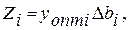 онда
онда

Барлығының бірдей пайдаға әсері:
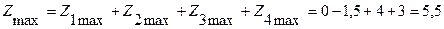 ақша бірлігі.
ақша бірлігі.
Егер шикізаттардың мөлшерлерінің өзгерістері қосалқы бағаларының тұрақтылық аралықтарында жатпаса, онда жаңа жуықталған бағаларды іздеу керек, яғни бағасының тұрақтылық аралығында жатпаған шикізаттың мөлшерін өзгертіп, қайтадан есепті симплекс әдісімен шығару қажет.
Фирмаға 4-ші бұйымды өндіруді жоспарға енгізудің ұтымдылығын бағалау үшін мына формуланы пайдаланамыз:

Сонымен, пайда (15 а.б.) шығыннан (10 а.б.) жоғары, сондықтан фирмаға 4-ші бұйымды өндіруді жоспарлағаны тиімді.
Дата добавления: 2015-11-18; просмотров: 2179;
