Равновесие химико-технологических процессов
Известно, что в зависимости от условий проведения, рассматриваемые химические взаимодействия могут протекать как в сторону образования продуктов, так и в сторону образования исходных веществ.
Если скорость образования продуктов численно равна скорости образования исходных веществ, то рассматриваемая система находится в состоянии равновесия.
(состояние равновесия—придуманное гипотетическое состояние). В учебниках будет нарисована колба с азотом и водородом, придавленная грузом, и сказано, что если оставить её на бесконечное время, то скорость взаимодействия азота и водорода будет равно скорости распада аммиака, то есть, таким образом, система будет находится в равновесии. С точки зрения логики, состояние равновесия важно, так как при протекании любых химико-технологических процессах мы можем подходить к состоянию равновесия, но не достигать его. Вывод: Построив реактор определенного размера, будем ли мы достигать требуемой производительности, и во что это выльется с точки зрения аппаратурного оформления? Необходимо научиться управлять состоянием равновесия. Первое решение, чтобы добиться производительности надо сместить равновесие в сторону продуктов, нужно только управлять состоянием равновесия, а достичь этого в реакторе невозможно, а лишь приблизиться. Ещё за счет равновесия можно блокировать побочные реакции.
Состояние равновесия характеризуется следующими свойствами:
1. Неизменность состояния равновесия при постоянстве внешних условий.
2. Подвижность равновесия.
Это свойство открыли одновременно двое ученых Ле Шателье и Браун.
Принцип Ле Шателье:
Если систему, находящуюся в равновесии, подвергнуть какому-либо внешнему воздействию, то система будет компенсировать это внешнее воздействие.
На основании этого принципа можно спрогнозировать смещение равновесия для единичной реакции. Если же реакций несколько, то спрогнозировать невозможно, можно только считать.
Если реакция экзотермическая (реакция с выделением теплоты), то с увеличением температуры равновесие смещается в сторону исходных веществ. (Соответственно с увеличением температуры система стремится скомпенсировать это увеличение за счет смещения равновесия). Если же реакция эндотермическая, то с увеличением температуры равновесие смещается в сторону продуктов.
Если реакция протекает с уменьшением объема газообразных реагентов, то при увеличении давления равновесие смещается в сторону продуктов реакции. Если же реакция протекает с увеличением объема, то при увеличении давления равновесие сместится в сторону исходных веществ. Если реакция протекает без изменения объема газообразных реагентов, то изменение давления не влияет на изменение состояния равновесия.
Введение в реакционную смесь дополнительного количества исходных веществ смещает равновесие в сторону образования продуктов. И наоборот, введение в реакционную смесь дополнительного количества продуктов смещает равновесие в сторону образования исходных веществ.
Введение в реакционную смесь дополнительного количества инерта смещает равновесие в сторону образования продуктов, если реакция идет с увеличением объема газообразных реагентов. Или в сторону образования исходных веществ, если же реакция идет с уменьшением объема газообразных реагентов.
В единичных реакциях можем предсказывать смещение равновесия.
3. В состоянии равновесия свободная энергия реагирования системы равна нулю. (Для изобарно-изотермического процесса энергия Гиббса(∆G)=0, для изохорно-изотермического процесса энергия Гельмгольца(∆F)=0).
Количественная оценка смещения равновесия.
aA+bB=cC+dD
∆G=dμD + cμC –aμA - bμB , где μ- химический потенциал.
μi = μi°+ RTlnPi, где Pi-парциальное давление (давление для одного компонента).
Pi= Pобщ·Zi , где Zi – мольная доля
Чтобы получить безразмерную величину используют приведенное давление: Р=P[атм]/1[атм]
∆G=dμD + cμC –aμA - bμB + RTln 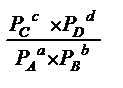
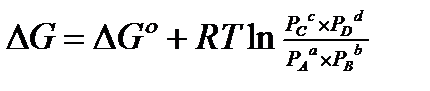
В состоянии равновесия скорость прямой реакции равна скорости обратной реакции.
 , то есть
, то есть  — на основании закона действующих масс.
— на основании закона действующих масс.
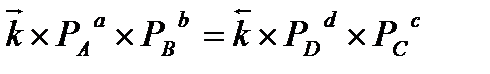 , где k-константа скорости
, где k-константа скорости
Уравнение Аррениуса: отношение констант скоростей прямой и обратной реакций есть отношение парциальных давлений.
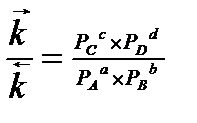
 , где Кр — термодинамическая константа равновесия.
, где Кр — термодинамическая константа равновесия.
Таким образом, получается, что термодинамическая константа равновесия равна отношению парциальных давлений.
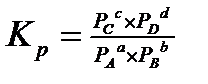
Используя закон Дальтона:
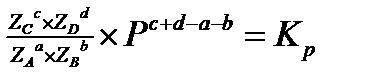
Уравнение для расчета равновесных мольных долей компонентов.
Эти расчеты помогают оценивать смещение равновесия численно при изменении внешних условий.
Используя эти данные и 3е свойство равновесия, имеем
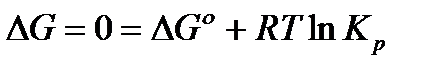
Зная, что 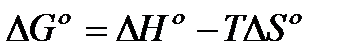 , получаем
, получаем
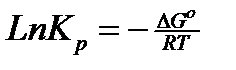
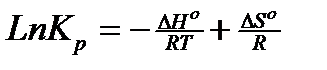 берем производную по температуре
берем производную по температуре
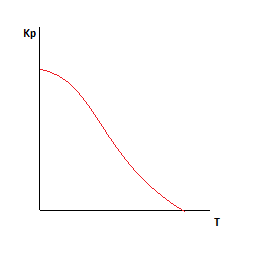
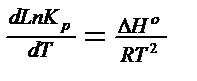 Изобара Вант-Гоффа.
Изобара Вант-Гоффа.
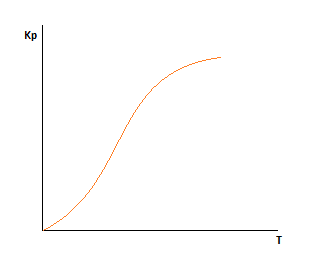
Исходя из уравнения, если реакция экзотермическая, то есть если 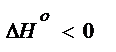 , то
, то 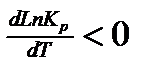 , следовательно, с увеличением температуры константа химической реакции уменьшается.
, следовательно, с увеличением температуры константа химической реакции уменьшается.
Если же реакция эндотермическая, то есть если 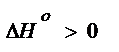 , то
, то 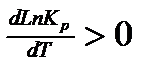 , следовательно, с увеличением температуры константа химической реакции увеличивается.
, следовательно, с увеличением температуры константа химической реакции увеличивается.
 Зная, что
Зная, что
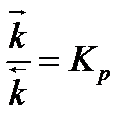 , получаем
, получаем
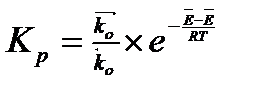 ,
,
где 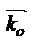 -предэкспоненциальный множитель константы скорости
-предэкспоненциальный множитель константы скорости
Е- энергия активации
Прологарифмируем
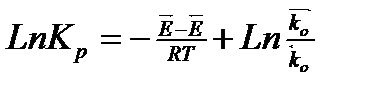 , таким образом
, таким образом
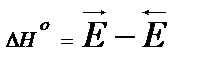 Изменение энтальпии в реакции в стандартных условиях (температура 25° и давление 1 атм) есть разность энергии активации прямой и обратной реакций, отсюда выводы:
Изменение энтальпии в реакции в стандартных условиях (температура 25° и давление 1 атм) есть разность энергии активации прямой и обратной реакций, отсюда выводы:
- Для экзотермической реакции энергия активации
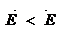 ;
; - Для эндотермической реакции
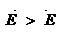 ;
; - Изменение Энергии активации прямой реакции влечет за собой изменение энергии активации обратной реакции;
- Катализатор не смещает равновесия;
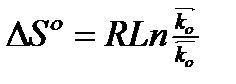 , k0 связан с энтропии реагирующей системы.
, k0 связан с энтропии реагирующей системы.
Кинетика химических реакций
Скорость химической реакции обозначается U.[U]=[кмоль/м3*с].
aA+bB→cC+dD
Вещество А всегда берётся в недостатке, а другие в избытке.
Скорость химической реакции оценивают по прореагировавшему веществу.
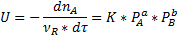
Где 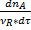 <0 для того чтобы U>0;
<0 для того чтобы U>0; 
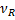 -объём реактора,
-объём реактора, 
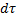 - время.
- время.
Скорость химической реакциичисленно равна изменениючисла молей ключевого компонента в единицу времени в единице объема реактора.
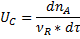
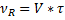
Где V-объёмный расход.
Скорости могут быть равны с учётом стехиометрии.
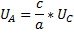
Скорость химической реакции пропорциональна движущей силе химической реакции (произведение концентрации исходных реагентов).
Уравнение Аррениуса.

Где К-константа скорости реакции
Произведение концентраций А и В- движущая сила химической реакции.
Формальная кинетикаисходит из того, что скорость пропорциональнадвижущей силе химической реакции.
Истинная кинетикаопределяет механическое протекание химической реакции со знанием всех законов протекания реакции.
Любая химическая реакция является многостадийной.
Пример-синтез аммиака:
3H2+N2↔2NH3(катализатор-железо)
1.N2+[cat]↔[N2]-самая медленная стадия. Происходит сорбция. Скорость химической реакции определяется поверхностью контакта фаз.
2.[N2]+H2↔[N2H3]
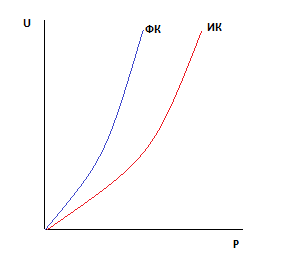 Отличие формальной кинетики от истинной.
Отличие формальной кинетики от истинной.
Формальная кинетика
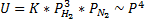
Истинная кинетика
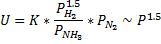
Закономерности сохраняются, численные значения другие.
Уравнение Аррениуса.
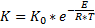
Чем больше температура, тем больше константа скорости К.
Дата добавления: 2015-11-12; просмотров: 3482;
