Понятие оптимизации. Критерии оптимизации

Оптимизация связана с необходимостью принятия решенияпо формированию реального объекта по данным научного исследования (любого, теоретического или экспериментального).

Оптимизация объекта – это выбор приемлемого (правильного решения), способ предпочтения одного варианта другим с учётом всех значащих факторов (переменных).

Величины, по которым осуществляется названный отбор, называются критериями оптимизации, устанавливающими ценность объекта.

Если критерий оптимизации учитывает один параметр выделения искомого варианта, то он называется частным критерием. Иногда один частный критерий недостаточен для установления истинной ценности объекта в рассматриваемых условиях. Тогда используются составные критерии(интегральные), каким- либо образом учитывающие все выбранные частные критерии для оценки. Частные критерии могут быть объективными, субъективными, детерминированными и статистическими.

Интегральные критерии могут быть трёх типов: аддитивными, мультипликативными, минимаксными (определяющими ценность объекта по принципу гарантированного успеха).

Аддитивные критерии - результат сложения нормированных частных критериев с использованием их весовых значений:

где c_i - весовой коэффициент какого-либо частного критерия; F_i(x) - абсолютное значение того же частного критерия; F_i⁰(x) - его нормирующая величина; f_i(x) - его нормированное значение.

Мультипликативные критерии используют принцип компенсации одного частного критерия другим путем суммирования не абсолютных, а относительных частных критериев типа

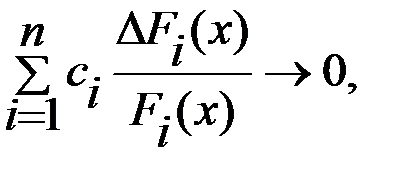
где ∆F_i(x) - изменение величины какого-то критерия по отношению к первоначальной его величине F_i(x).

Если принять ∆F_i(x)<<F_i(x), то можно представить мультипликативный критерий в интегральной форме в виде произведения

При пользовании мультипликативным критерием отпадает необходимость нормирования частных критериев. Результаты оптимизации по аддитивному и мультипликативному критериям оказываются разными. Выбор того или другого при анализе ММ (математической модели) должен определяться конкретными условиями функционирования объекта.

Минимаксные критерии принцип компромисса основывают на идее равномерности частных критериев. Идея равномерного компромисса состоит в создании условий, при которых частные критерии с учетом весовых коэффициентов становятся равными:

c_if_i(x)=k.

При большом числе частных критериев точно сделать это практически невозможно. В такой ситуации может быть использован принцип максиминизации, последовательного подтягивания наименьших нормализованных частных критериев до уровня достаточно высоких. Эта операция отрицательно сказывается на остальных частных критериях. Проведение ряда шагов такого счета позволяет во многих случаях достигнуть приемлемого уравнивания противоречивых частных критериев.

Математически этот принцип формируется следующим образом: оптимальный набор частных критериев реализуется в виде максимума из минимальных значений этих критериев. Формальная запись: существует Х⁰ 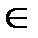Х такой, что F(X⁰)= 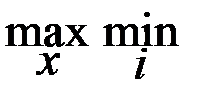(x), где i=1,…n (вектор), а X={х₁,х₂,…,х_n}. Такой принцип выбора носит еще название принципа гарантированного результата.

Значения весовых коэффициентов c_i устанавливают на основе современного уровня развития отрасли, отношений, к которым относится математическая модель, путем сравнения существующих объектов. Формальный метод определения этих коэффициентов и состоит в решении обратной задачи: по ценности объекта производится вычисление коэффициентов. Задача не из легких.

ОБЩИЕ ВОПРОСЫ ТЕОРИИ МОДЕЛИРОВАНИЯ