Показатели устойчивости системы.

В плоскости корней характеристического уравнения АСР границей устойчивости является мнимая ось этой плоскости. Удаленность корней от мнимой оси определяет запас устойчивости. Так запас устойчивости может быть охарактеризован расстоянием 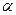от мнимой оси ближайшей к ней пары комплексных сопряженных корней (Рис. 5.9).

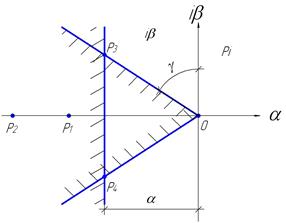
Рис. 5.9 Граница устойчивости на плоскости корней.

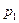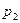Здесь и - действительные отрицательные корни, и 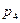- комплексные сопряженные корни

Это расстояние называется степенью устойчивости. Запас устойчивости системы характеризуется так же углом 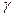, составленным мнимой осью с лучом, соединяющим ближайшим комплексный корень с началом координат плоскости корней. Тангенс этого угла называется степенью колебательности этой системы, а синус –коэффициентом затухания для переходных процессов системы регулирования.

Если свойства системы заданы частотными характеристиками, (Рис. 5.10) то запас устойчивости удобно характеризовать удаленностью АФХ разомкнутой системы регулирования от точки с координатами 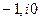комплексной плоскости 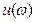, 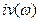. Запас устойчивости характеризуется двумя численными величинами: запасом устойчивости системы по модулю и запасом ее устойчивости по фазе.

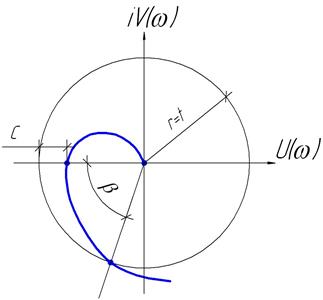
Рис. 5.10 Амплитудно-фазовая характеристика разомкнутой системы.

Запас устойчивости по модулю определяется величиной отрезка 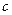- расстояние от точки с координатами 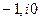до точки пересечения АФХ с отрицательной действительной полуосью. Запас устойчивости по фазе характеризуется величиной угла 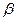, который образован отрицательной действительной полуосью и лучом, соединяющим начало координат с точкой пересечения АФХ с окружностью радиусом 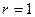с центром в начале координат плоскости. Эта величина показывает, насколько должно увеличится отставание по фазе выходного сигнала в разомкнутой системе , что бы замкнутая АСР оказалась на границе устойчивости.