Пример аналогового моделирования двигателя постоянного тока
Пусть имеем двигатель постоянного тока (ДПТ) независимого возбуждения, скорость которого регулируется изменением напряжения на якоре.
Исходные данные для аналогового моделирования:
1. Уравнение описывающее якорную цепь ДПТ:
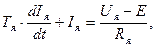(35)
где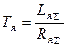 
- постоянная времени якоря;
Е=сеФ w - ЭДС наводимая в обмотке якоря при его вращении.
2. Уравнение движения:
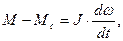(36)
где М=смФJя - электромагнитный момент двигателя;
Мс - момент сопротивления (нагрузки);
J - суммарный момент инерции.
Так как выражения М-Мс и I-Ic тождественно равны, то уравнение движения можно переписать в следующем виде:
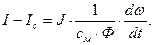(37)
Умножим и разделим выражение (37) на смФ и Rя :
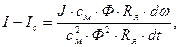(38)
где выражение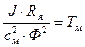 
- механическая постоянная времени.
Уравнение движения с учётом введённых поправок:
(39)
Переходим к операторной форме записи, заменяя дифференциал 
на оператор Лапласа.
Уравнение якорной цепи:
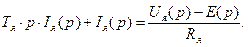(40)
Уравнение движения:
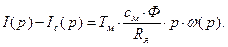(41)
Преобразуем форму записи уравнений (40) и (41) с тем, чтобы получить передаточные функции якорной цепи и механического звена:
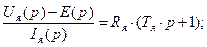(42)
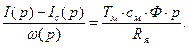(43)
Так как выражение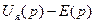 
- входное воздействие на якорную цепь (аналогично для механического звен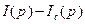а 
), а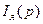 
( 
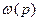) – выходные координаты, то передаточные функции звеньев запишутся так:
· Для якорной цепи:
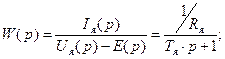(44)
· Для механической части:
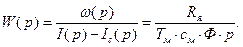(45)
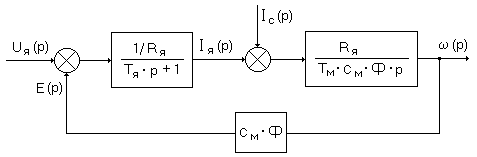
На основании полученных передаточных функций построим структурную схему двигателя постоянного тока независимого возбуждения (ДПТ НВ).
|
Рис. 39 Структурная сема ДПТ НВ.
По структурной схеме из операционных блоков собирают аналоговую модель ДПТ НВ.
Этапы создания аналоговой модели.
1. Масштабирование параметров Iя , w , t, Uя :
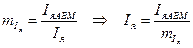(46)
где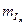 
- масштаб тока якоря;
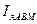- значение тока якоря используемое в АВМ;
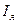- истинное значение физической величины.
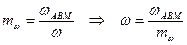(47)
где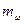 
- масштаб угловой скорости вращения якоря;
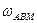- значение угловой скорости используемое в АВМ;
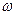- истинное значение скорости вращения якоря.
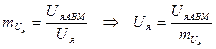(48)
где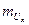 
- масштаб напряжения на якоре;
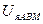- значение напряжения на якоре используемое в АВМ;
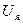- истинное значение физической величины.
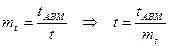(49)
где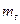 
- масштаб времени моделирования;
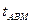- значение времени моделирования используемое в АВМ;
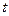- истинное значение физической величины.
2. Преобразование уравнений (40) и (41) в удобную форму для моделирования на АВМ:
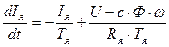(50)
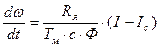(51)
3. Переход к уравнениям с маштабами:
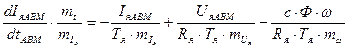(52)
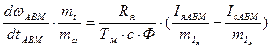(53)
Производим упрощения в формулах (52), (53) и окончательно получают уравнения используемые в аналоговом моделировании.
(54)
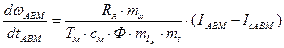(55)
4. Составляем схему набора АВМ:
|
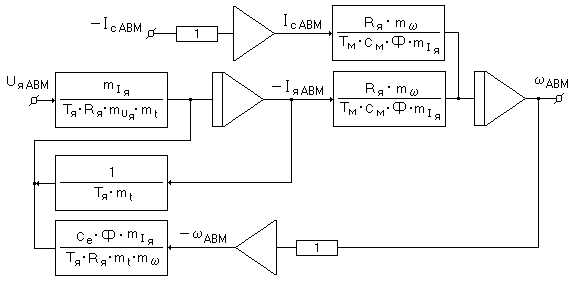
Рис. 40 Схема набора на АВМ модели ДПТ НВ.
Дата добавления: 2015-11-10; просмотров: 956;