ПОНЯТИЕ О НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЯХ
Неравноточными измерениями называются такие, которые выполнены различным числом приемов, приборами различной точности и т. д.
Если измерения неодинаковой точности, то для определения общей арифметической средины пользуются формулой:
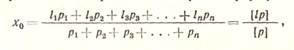 (28)
(28)
где pi, р2, Рз, ..., р« — соответствующие веса неравноточных
измерений U, h, h, ..., ln-
Весом называется число, которое выражает степень доверия к результату измерения. Для удобства вычислений веса можно увеличивать или уменьшать в одинаковое число раз.
В тех случаях, когда неизвестны веса измеренных величин, а известны их средние квадратические ошибки, то веса можно вычислить по формуле
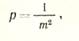 (29)
(29)
т. е. вес результата измерений обратно пропорционален квадрату средней квадратической ошибки.
При неравноточных измерениях средняя квадратическая ошибка измерения, вес которого равен единице, определяется по формуле:
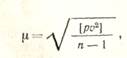 (30)
(30)
где v — разность между отдельными результатами измерений и общей арифметической срединой.
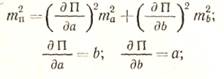
Таблица 2
| № п/п | Угол р | Число приемов | Вес р | а" | pv | pv? |
| 60°25'12" 60 25 06 60 25 15 | +2 -4 +5 | +2 -12 + 10 | ||||
| X0 | 60 25 10 | [р]=6 | [pv] = 0 | [pv2] = = 102 |
Средняя квадратическая ошибка общей арифметической средины вычисляется по формуле:
(31)
Пример. Угол измерен три раза различным числом приемов. Определить вероятнейшее значение угла, среднюю квад-ратическую ошибку единицы веса и среднюю квадратическую ошибку общей арифметической средины.
Вычисления показаны в табл. 2.
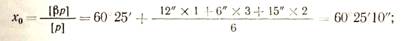
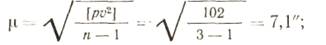
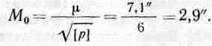
О точности вычислений. Точность, полученная при измерении, должна сохраняться и при вычислениях. Поэтому вычисления ведутся на один десятичный знак больше, чем измерения, или в отдельных случаях с таким же числом десятичных знаков.
Если при вычислениях получено число с большим количеством знаков, чем это требуется, то производится его округление например, 12,46=12,5; 16,64=16,6; 120,455=120,46;122,525=122,52. В последних двух и аналогичных случаях округление производится до четных.
При сложении и вычитании приближенных чисел сохраняют столько десятичных знаков, сколько их имеется в числе с наименьшим количеством десятичных знаков плюс один запасной.Например,
72,5
+ 2,07
0,224
74,794 .
Полученный результат округляют до двух десятичных знаков—74,79.
При умножении двух приближенных чисел в результате оставляют столько десятичных знаков, сколько их в числе, у которого меньше значащих цифр, чем у остальных, плюс один.
Например, 66,34X0,218= 14,46212^ 14,46.
При делении двух приближенных чисел в частном оставляют столько знаков, сколько их в числе, имеющем меньшее количество значащих цифр, плюс один.
Например, 420,45: 31,3= 13,432 907«13,43.
При извлечении квадратного корня из приближенного числа в результате оставляют столько значащих цифр, сколько их имеет подкоренное выражение.
Например,
√32,7 = 5,7183913 = 5,72.
Топографические планы и карты
Понятие о плане и карте
При изображении участка земной поверхности радиусом до 10 км его проектируют на горизонтальную плоскость. Полученное горизонтальное проложение участка в уменьшенном виде наносят на бумагу. Таким образом, чертёж, дающий в подобном уменьшенном виде изображение горизонтального проложения участка местности, называется планом. При изображении на плоскости значительных территорий проектирование их производят на сферическую поверхность, которую затем развертывают в плоскость. В этом случае участки местности изображаются с определенными искажениями. Для уменьшения этих искажений применяют специальные методы построений, называемые картографическими проекциями. В выбранной проекции по определенным математическим законам строят географическую сетку меридианов и параллелей, называемую картографической сеткой, внутри которой располагают изображения элементов местности – контуров и рельефов. Такое построение называется картой. Таким образом, карта – это уменьшенное изображение на плоскости значительного участка земной поверхности, полученное с учетом кривизны Земли. Планы и карты с изображением на них контуров рельефа и местности называются топографическими, планы с изображением только контуров называются ситуационными или контурными.
Для построения линейного масштаба вычерчивают прямую линию и делят её на ряд равных отрезков, называемых основанием масштаба. Обычно основание масштаба делают равным 2 см. крайний левый отрезок делят дополнительно на 10 частей. Концы отрезков подписывают количеством метров или километров на местности ,в соответствующим в данном масштабе расстоянию данного штриха от нулевого. За нулевой штрих принимают правый конец первого отрезка .На рис.6,а изображён линейный масштаб для численного масштаба 1:10000.
За критерий точности, с которой можно определить длины линий, пользуясь поперечным масштабом (рис. 6,в ), берётся величина, равная 0,1 мм, соответствующая наименьшему расстоянию, различаемому невооруженным глазом. Расстояние на местности, соответствующее в заданном масштабе 0,1 мм на карте, называется точностью масштаба. Следовательно, на карте масштаба 1:10000 можно откладывать и измерять расстояния с точностью 1 м.
Топографические планы создаются в крупных масштабах, а именно: 1:500, 1:1000, 1:2000 и 1:5000. Эти планы предназначаются для составления генеральных планов, технических проектов и рабочих чертежей при строительстве различных инженерных сооружений.
Карты по масштабам подразделяются на крупномасштабные – 1:10 000, 1:25 000, 1:50 000, среднемасштабные – 1:200 000, 1:300 000 и 1:500 000, и мелкомасштабные, начиная с 1:1 000 000.
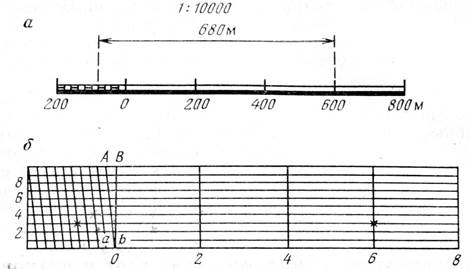
Рис. 6. Масштабы: а – линейный ; в – поперечный.
Номенклатура топографических карт и планов
Для удобства использования топографических карт и планов разного масштаба в Российской Федерации используется их разделение на отдельные листы. Это разделение называется разграфкой. При этом система обозначений отдельных листов называется номенклатурой. За основу разграфки и номенклатуры принята карта масштаба 1:1 000 000. Для получения отдельных листов этой карты земной шар делится меридианами через 6О на колонны и параллелями через 4О на ряды. Колонны нумеруются арабскими цифрами от 1 до 60 с запада на восток от меридиана с долготой 180О. Ряды обозначаются заглавными буквами латинского алфавита от А,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P,Q,R,S,T,U,V, начиная от экватора к северному и южному полюсу (Рис. 7.) Таким образом, на одном листе карты данного масштаба изображается каждый из 266 участков земной поверхности. При этом номенклатура отдельного листа складывается из латинской буквы, обозначающей ряд и цифры, соответствующей номеру колонны. Например, А-1. Номенклатура листов топографических карт и планов более крупных масштабов определяется следующим образом. Каждому листу карты масштаба 1:1 000 000 соответствуют 144 листа карты масштаба 1: 100 000, которые обозначаются арабскими цифрами (Рис.8,а) по порядку с левого верхнего угла, имеющего № 1 до правого нижнего угла, имеющего № 144. При этом номенклатура такого листа образуется прибавлением соответствующей цифры к номенклатуре листа карты 1: 1 000 000. Например, А-1-120. 4 листа карт масштаба 1:50 000, соответствуют одно
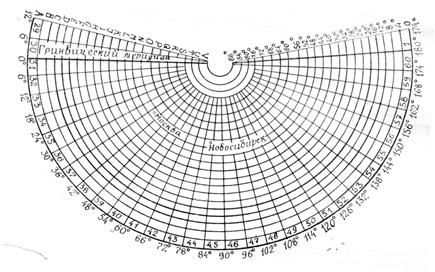 |
Рис. 7 .Схема разграфки и номенклатуры листов карт масштаба 1 : 1000000.
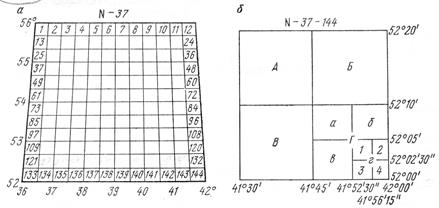 |
Рис.8. Разграфка и номенклатура топографических карт масштабов 1:100000; 1: 50000; 1: 25000 ; 1: 10000.
му листу карты масштаба 1: 100 000. Каждый лист карты масштаба 1: 50 000 обозначается приписыванием к номенклатуре карты масштаба 1:100 000 одной из четырех заглавных букв русского алфавита А, Б, В, Г (Рис.8,б). Например, А-1-120-Б. Одному листу карты масштаба 1:50 000 соответствует 4 листа карты масштаба 1:25 000, которые обозначаются строчными буквами а,б,в,г. Например, А-1-120-Б-в. Четыре листа карты масштаба 1:10 000 обозначаются цифрами 1,2,3,4, приписываемыми к номенклатуре масштаба 1:25 000, А-1-120-Б-в-3. Планы и участки, площадью до 20 км2 могут быть разграфлены с помощью прямоугольника. В основу разграфки в этом случае положен лист плана масштаба 1:5000 с размерами рамки 40×40 см. Листы плана масштаба 1:5000 нумеруются арабским цифрами (Рис. 9) .
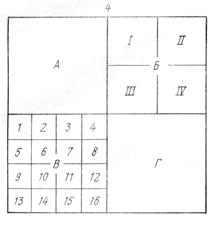
Рис.9.Примоугольная разграфка и номенклатура листов планов масштабов
Рельеф земной поверхности на планах и картах
Совокупность неровностей поверхности земли называется рельефом. В геодезии выделяют следующие основные формы рельефа:
Гора –возвышенность в виде купола или конуса. Гора имеет вершину и склоны, а также подошву – линию, отделяющую склоны от равнины. Возвышенности ниже 200 м относительно местности называют холмом.
Котловина – чашеобразная вогнутая часть земной поверхности, имеющая дно и скаты, а также бровку, то есть линию перехода скатов в равнину. Небольшая котловина называется впадиной.
Хребет –возвышенность, вытянутая в одном направлении, имеющая водораздельную линию, которая соединяет наиболее высокие точки хребта.
Лощина –противоположное хребту углубление, вытянутое в одном направлении.
Седловина –перегиб хребта между двумя вершинами.
Дата добавления: 2015-11-10; просмотров: 1454;
