Второй способ расчета по критерию U

Преимущество второго способа подсчета по критерию U наи­более отчетливо проявляется в тех случаях, когда две или боль­шее количество одинаковых величин будут входить в оба сравни­ваемых ряда.

В условиях задачи 7 несколько изменим экспери­ментальные данные таким образом, чтобы в обеих выборках имелись одинаковые значения. Представим эти измененные дан­ные в виде таблицы 9*.

Таблица 9*.

№1	№2	№3	№4
Группа с дополнительной мотивацией Х	Группа без дополнительной мотивации У	Ранги	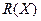Ранги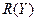
	-		-
-		-
	-	(3) 3,5	-
	-	(4) 3,5	-
	-	(5) 5,5	-
-		-	(6) 5,5
-		-
	-		-
	-	(9) 10,5	-
-		-	(10) 10,5
-		-	(11) 10,5
	-	(12) 10,5	-
	-		-
-		-
-		-
-		-
-		-
Сумма инверсий		55,5	97,5

Исходные данные 9* располагаются так же, как и в табли­це 9. Затем в двух столбцах проставляются ранги, так, как буд­то бы оба столбца образуют собой один упорядоченный ряд чи­сел. Подчеркнем, однако, что ранги для чисел первого столбца помещаются в третий столбец, а ранги чисел второго столбца - в четвертый. По каждому столбцу в отдельности подсчитываются суммы рангов.

Следующим этапом, как обычно при ранжировании, являет­ся проверка его правильности. Для этого:

1. Подсчитывается общая сумма рангов из таблицы 9*:

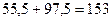
2. Рассчитывается сумма рангов по формуле:

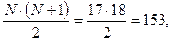где .

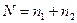Поскольку расчетные суммы случаев совпали, то ранжирова­ние было проведено правильно.

3. Затем находится наибольшая по величине ранговая сумма. Она обозначается как 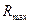. В нашем случае она равна 97,5.

4. 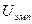вычисляется по следующей формуле:

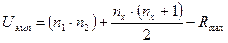
где 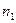- численное значение первой выборки,

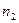- численное значение второй выборки,

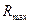-наибольшая по величине сумма рангов,

- количество испытуемых в группе с большей суммой рангов.

Подсчитываем величину :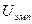

.

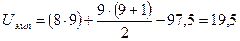Величины критических значений уже найдены нами при рас­чете первым способом по таблице 7 Приложения, поэтому сразу строим «ось значимости», которая имеет следующий вид:

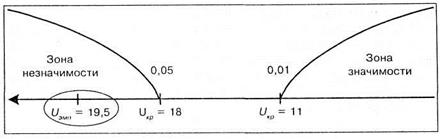
Несмотря на то, что мы немножко «подправили» эксперимен­тальные данные для получения одинаковых чисел в обоих столб­цах, рассчитанное значение 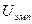вновь попало в зону незначимо­сти, следовательно, принимается гипотеза 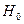о сходстве. Тем са­мым психолог может утверждать, что мотивация не приводит к статистически значимому увеличению эффективности времени решения технической задачи.

Ниже представлен алгоритм подсчета критерия по второму способу.