Первый способ расчета по критерию U
Полученные данные необходимо объединить, т.е. представить как один ряд и упорядочить его по возрастанию входящих в него величин. Подчеркнем, что для критерия U важны не сами численные значения данных, а порядок их расположения. Предварительно обозначим каждый элемент первой группы символом х, а второй — символом у. Тогда общий упорядоченный по возрастанию численных величин ряд можно представить так:
х у х х х у у х х у у х х у у у у
6 8 25 25 30 31 32 38 39 41 41 43 44 45 46 50 55 (*)
Если бы упорядоченный ряд, составленный по данным двух выборок, принял бы такой вид:
х х х х х х х х
у у у у у у у у у (**)
то, очевидно, что такие две выборки значимо различались бы между собой (как, например, различаются в классе двоечники и отличники). Расположение (**) называется идеальным. Критерий U основан на подсчете нарушений в расположении чисел в упорядоченном экспериментальном ряду по сравнению с идеальным рядом. Любое нарушение порядка идеального ряда называют инверсией. Одним нарушением (одной инверсией) считают такое расположение чисел, когда перед некоторым числом первого ряда, стоит только одно число второго ряда. Если перед некоторым числом первого ряда стоят два числа второго ряда — то возникают две инверсии и т.д.
Удобно подсчитывать число инверсий, расположив исходные данные в виде таблицы, в которой один столбец состоит из данных первого ряда, а второй из данных второго. При этом и первый и второй столбцы имеют пропуски чисел, которые обозначаются символом « - ».
Пропуск в первом столбце означает, что в соседнем столбце имеется число, занимающее промежуточное положение по отношению к числам первого столбца, ограничивающим пропуск. То же самое верно для пропусков второго столбца. Упорядоченное объединение экспериментальных данных в порядке их возрастания, представленное отдельно в первом и втором столбце с учетом пропусков и является по существу модифицированным рядом (*).
Представим этот модифицированный ряд в виде таблицы 9, в которую добавлены еще два столбца для подсчета инверсий. В третьем столбце таблицы даны инверсии первого столбца по отношению ко второму, они обозначаются как инверсии X/Y, а в четвертом столбце инверсии второго столбца по отношению к первому, они обозначаются как инверсии Y/X.
Таблица 9.
| №1 | №2 | №3 | №4 |
| Группа с дополнительной мотивацией Х | Группа без дополнительной мотивации У | Инверсии X/Y | Инверсии Y/X |
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| - | - | ||
| Сумма инверсий |
Инверсии X/Y подсчитываются следующим образом:
число 6 первого столбца не имеет перед собой никаких чисел второго столбца, поэтому в третьем столбце напротив числа 6 ставим 0;
числа 25, 25 и 30 первого столбца (Х)имеют перед собой только одно число второго столбца - 8 (У), т.е. имеют по одной инверсии, поэтому в столбце 3 для инверсий X/Y каждому из чисел 25, 25 и 30 ставим в соответствие число 1;
числа 38 и 39 первого столбца имеют перед собой по три числа второго столбца - это числа 8, 31 и 32, т.е. имеют по три инверсии;
последние два числа первого столбца 43 и 44 имеют перед собой 5 чисел второго столбца, т.е. по 5 инверсий.
Таким образом, суммарное число инверсий Х/У третьего столбца составляет:
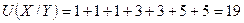 .
.
Необходимо рассчитать также число инверсий второго столбца (У)по отношению к первому (Х),т.е. суммарное число инверсий Y/X. Поскольку число 8 (У)) имеет перед собой одно число первого столбца - 6, то в столбце 4 с инверсиями для Y/X напротив числа 8 ставим число инверсий - 1;
числа 31 и 32 второго столбца имеют перед собой четыре числа первого столбца: 6, 25, 25 и 30, следовательно, числу 31 и числу 32 приписываем в столбце 4 величины инверсий равные 4, и так далее. Таким образом, суммарное число инверсий Y/X четвертого столбца составляет:
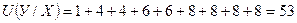 .
.
Видно, что во втором случае сумма инверсий существенно больше. Принято считать, что 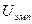 есть минимальная из сумм инверсий.
есть минимальная из сумм инверсий.
Или, иначе говоря, 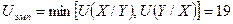
Получив 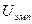 , обращаемся к таблице 7 Приложения. Эта таблица, в отличие от предыдущих, состоит из нескольких таблиц, рассчитанных отдельно для уровней Р = 0,05, Р = 0,01, а также для величин
, обращаемся к таблице 7 Приложения. Эта таблица, в отличие от предыдущих, состоит из нескольких таблиц, рассчитанных отдельно для уровней Р = 0,05, Р = 0,01, а также для величин 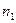 и
и 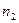 . В нашем случае:
. В нашем случае: 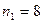 и
и 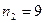 . По этим таблицам находим, что значения
. По этим таблицам находим, что значения 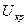 равны:
равны:
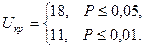
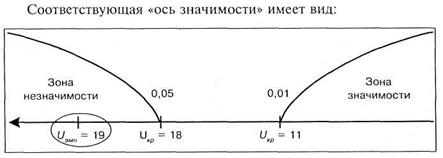
Полученное значение 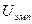 попало в зону незначимости, следовательно, принимается гипотеза
попало в зону незначимости, следовательно, принимается гипотеза 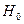 о сходстве, а гипотеза
о сходстве, а гипотеза 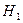 о наличии различий отклоняется. Таким образом, психолог может утверждать, что дополнительная мотивация не приводит к статистически значимому увеличению эффективности решения технической задачи.
о наличии различий отклоняется. Таким образом, психолог может утверждать, что дополнительная мотивация не приводит к статистически значимому увеличению эффективности решения технической задачи.
Дата добавления: 2015-08-21; просмотров: 871;
