Простой трубопровод постоянного сечения
Жидкость по трубопроводу движется благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Этот перепад уровней энергии может создаваться несколькими способами: работой насоса, разностью уровней жидкости, давлением газа.
Рассмотрим простой трубопровод постоянного сечения, который расположен произвольно в пространстве (рисунок 4.1), имеет общую длину 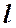 и диаметр d, а также содержит ряд местных сопротивлений (вентиль, фильтр и обратный клапан).
и диаметр d, а также содержит ряд местных сопротивлений (вентиль, фильтр и обратный клапан).
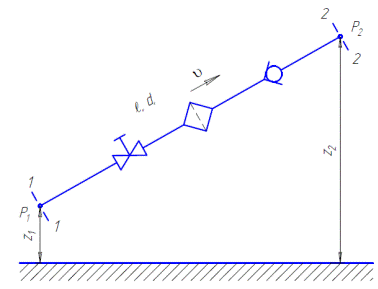
Рисунок 4.1 ─ Схема простого трубопровода
В начальном сечении трубопровода 1-1геометрическая высота равна 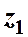 и избыточное давление
и избыточное давление 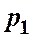 , а в конечном сечении 2-2 ─ соответственно
, а в конечном сечении 2-2 ─ соответственно 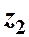 и
и 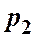 . Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна
. Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна 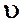 .
.
Запишем уравнение Бернулли для сечений 1-1 и 2-2. Поскольку скорость в обоих сечениях одинакова и 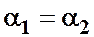 , то скоростной напор можно не учитывать. При этом получим
, то скоростной напор можно не учитывать. При этом получим
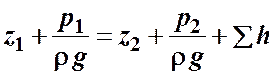
или
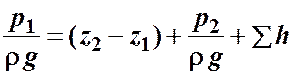 . (4.1)
. (4.1)
Пьезометрическую высоту, стоящую в левой части уравнения, назовем потребным напором 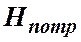 . Если же эта пьезометрическая высота задана, то ее называют располагаемым напором
. Если же эта пьезометрическая высота задана, то ее называют располагаемым напором 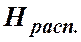 .
.
Такой напор складывается из геометрической высоты 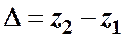 , на которую поднимается жидкость, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе.
, на которую поднимается жидкость, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе.
Назовем сумму первых двух слагаемых статическим напором, который представим как некоторую эквивалентную геометрическую высоту
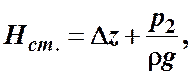
а последнее слагаемое 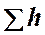 ─ как степенную функцию расхода
─ как степенную функцию расхода
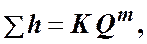
тогда
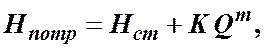 (4.2)
(4.2)
где 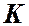 ─ величина, называемая сопротивлением трубопровода;
─ величина, называемая сопротивлением трубопровода;
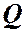 ─расход жидкости;
─расход жидкости;
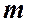 ─ показатель степени, который имеет разные значения в зависимости от режима течения.
─ показатель степени, который имеет разные значения в зависимости от режима течения.
Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление трубопровода равно
 и
и 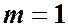 , (4.3)
, (4.3)
где 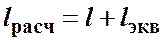 .
.
Численные значения эквивалентных длин  для различных местных сопротивлений обычно находят опытным путем.
для различных местных сопротивлений обычно находят опытным путем.
Для турбулентного течения, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход, получаем
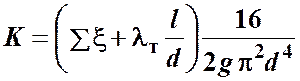 и
и 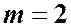 . (4.4)
. (4.4)
Формула (4.2), дополненная выражениями (4.3) и (4.4) является основной для расчета простых трубопроводов. По ней можно построить кривую потребного напора в зависимости от расхода. Чем больше расход Q, который необходимо обеспечить в трубопроводе, тем больше требуется потребный напор Нпотр.
При ламинарном течении эта кривая изображается прямой линией (рис.4.2, а), при турбулентном ─ параболой с показателем степени равном двум (рис.4.2, б).

Рисунок 4.2─ Зависимости потребных напоров от расхода жидкости в трубопроводе
Крутизна кривых потребного напора зависит от сопротивления трубопровода Kи возрастает с увеличением длины трубопровода и уменьшением диаметра, а также с увеличением местных гидравлических сопротивлений.
Величина статического напора Нстположительна в том случае, когда жидкость движется вверх или в полость с повышенным давлением, и отрицательна при опускании жидкости или движении в полость с пониженным давлением. Точка пересечения кривой потребного напора с осью абсцисс (точка А) определяет расход при движении жидкости самотеком. Потребный напор в этом случае равен нулю.
Иногда вместо кривых потребного напора удобнее пользоваться характеристиками трубопровода.
Характеристикой трубопроводаназывается зависимость суммарной потери напора (или давления) в трубопроводе от расхода:
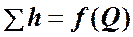 .
.
Дата добавления: 2015-08-21; просмотров: 842;
