Последовательное соединение. Возьмем несколько труб различной длины, разного диаметра и содержащих разные местные сопротивления, и соединим их последовательно (рисунок 4.3

Возьмем несколько труб различной длины, разного диаметра и содержащих разные местные сопротивления, и соединим их последовательно (рисунок 4.3, а).

Рисунок 4.3─ Последовательное соединение трубопроводов

При подаче жидкости по такому составному трубопроводу от точки Мк точке Nрасход жидкости Qво всех последовательно соединенных трубах 1, 2 и 3 будет одинаков, а полная потеря напора между точками Ми Nравна сумме потерь напора во всех последовательно соединенных трубах. Таким образом, для последовательного соединения имеем следующие основные уравнения:

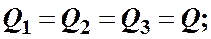
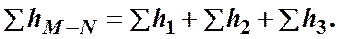(4.5)

Эти уравнения определяют правила построения характеристик последовательного соединения труб (рисунок 4.3, б). Если известны характеристики каждого трубопровода, то по ним можно построить характеристику всего последовательного соединения M-N. Для этого нужно сложить ординаты всех трех кривых.

Параллельное соединение

Такое соединение показано на рисунке 4.4, а. Трубопроводы 1, 2 и 3 расположены горизонтально.

Рисунок 4.4 ─ Параллельное соединение трубопроводов

Обозначим полные напоры в точках МиNсоответственно H_Mи H_N, расход в основной магистрали (т.е. до разветвления и после слияния) ─ через Q, а в параллельных трубопроводах через 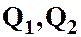и 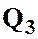; суммарные потери в этих трубопроводах через 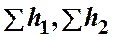и .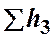

Очевидно, что расход жидкости в основной магистрали

(4.6)

Выразим потери напора в каждом из трубопроводов через полные напоры в точках Ми N:

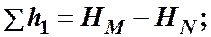
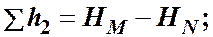
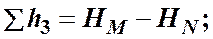
Отсюда делаем вывод, что

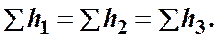(4.7)

т.е. потери напора в параллельных трубопроводах равны между собой.

Их можно выразить в общем виде через соответствующие расходы следующим образом

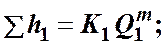
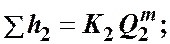
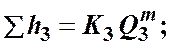
где Kиm - определяются в зависимости от режима течения формулами (4.3) и (4.4).

Из уравнений (4.6) и (4.7) вытекает следующее правило: для построения характеристики параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при одинаковых ординатах ( 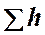). Пример такого построения дан на рисунке 4.3, б.