Потери напора на местные сопротивления

Местные потери напора обусловливаются преодолением местных сопротивлений, создаваемых фасонными частями, арматурой и прочим оборудованием трубопроводных сетей. Местные сопротивления вызывают изменение величины или направления скорости движения жидкости на отдельных участках трубопровода, что связано с появлением дополнительных потерь напора. Движение в трубопроводе при наличии местных сопротивлений является неравномерным. Потери напора в местных сопротивлениях 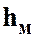(местные потери напора) вычисляют по формуле Вейсбаха:

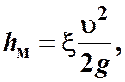(3.22)

где 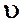— средняя скорость в сечении, как правило, расположенном ниже по течению за данным сопротивлением; 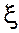— безразмерный коэффициент местного сопротивления. Для определения потерь давления 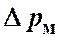формула (3.29) преобразуется к виду:

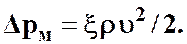(3.23)

Значения коэффициентов местных сопротивлений зависят от конфигурации местного сопротивления и режима потока, подходящего к сопротивлению; этот режим определяется коэффициентом гидравлического трения 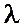подходящего потока, т.е. числом Рейнольдса и относительной шероховатостью.

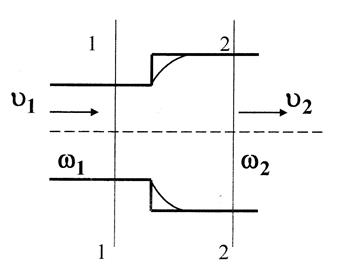Внезапное расширение трубопровода

Рисунок 3.6 ─ Внезапное расширение трубопровода

Потери напора при внезапном расширении трубопровода находят по формуле Борда:

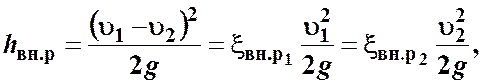(3.24)

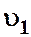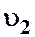где и — средние скорости течения соответственно до и после расширения.

Таким образом, потеря напора при внезапном расширении трубопровода равна скоростному напору от потерянной скорости.

Коэффициент местного сопротивления в формуле Вейсбаха (3.29) определяется выражениями:

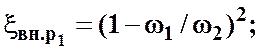(3.25)

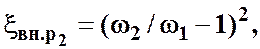(3.26)

где 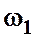и 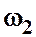— площади сечений трубопровода соответственно до и после расширения.