Потери напора по длине

При равномерном движении в трубах потери напора по длине, как при турбулентном, так и при ламинарном движении определяются для круглых труб по формуле Дарси

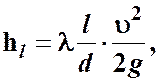(3.11)

а для труб любой другой формы сечения по формуле

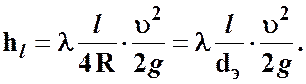(3.12)

В некоторых случаях также используют формулу

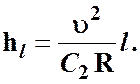(3.13)

Потери давления на трение по длине 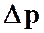, Па, определяются по формуле

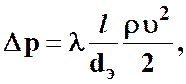(3.14)

где 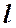─ длина участка трубы или канала, м;

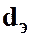─ эквивалентный диаметр, м;

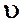─ средняя скорость течения, м/с;

─ гидравлический радиус трубы, м;

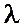─ коэффициент гидравлического трения;

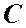─ коэффициент Шези, связанный с коэффициентом гидравлического трения зависимостями

;

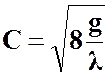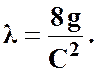
В зависимости от режима движения применяются различные формулы для определения коэффициента гидравлического трения.

При ламинарном движении по трубам круглого сечения коэффициент гидравлического трения определяется по формуле

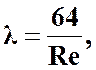(3.15)

а для труб любой формы сечения

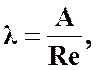(3.16)

где А ─ коэффициент, численное значение которого зависит от формы поперечного сечения трубы.

Тогда формула для определения потерь напора по длине при ламинарном режиме принимает вид

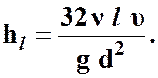(3.17)

Впервые наиболее исчерпывающие работы по определению 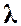были даны И.И. Никурадзе, который на основе опытных данных построил график зависимости от 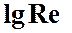для ряда значений 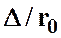. Опыты Никурадзе были проведены на трубах с искусственно заданной шероховатостью, полученной путем приклейки песчинок определенного размера на внутренние стенки трубопровода. Результаты этих исследований представлены на рисунке 3.5, где построены зависимости от 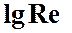для ряда значений .

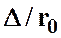Прямая I соответствует ламинарному режиму движения жидкости в соответствии с выражением (3.15).

При турбулентном режиме различают три области гидравлических сопротивлений, установленных в результате опытов, проведенных Никурадзе (см. рисунок 3.5)

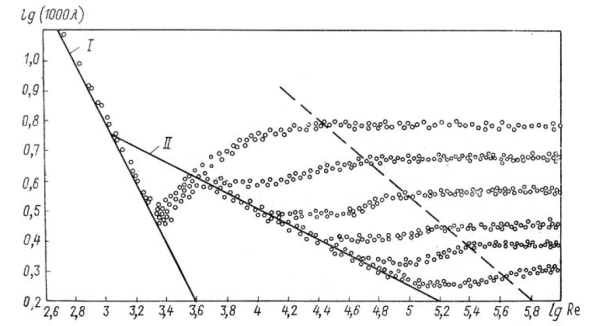
Рисунок 3.5 ─ График Никурадзе

Первая область ─ область малых 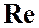и 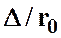, где коэффициент 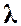не зависит от шероховатости, а определяется лишь числом 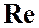(отмечена на рисунке 3.5 прямой II).

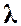Это область гидравлически гладких труб. Если число Рейнольдса лежит в диапазоне коэффициент определяется по полуэмпирической формуле Блазиуса

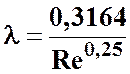. (3.18)

или по формуле П.Н. Конакова

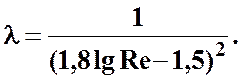(3.19)

Во второй области, расположенной между линий II и пунктирной линией справа, коэффициент 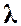зависит одновременно от двух параметров ─ числа 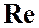и относительной шероховатости 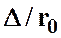, которую можно заменить на 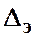. Для определения в этой области может служить универсальная формула А.Д. Альтшуля

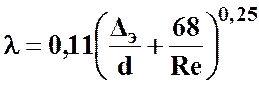. (3.20)

где 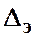─ эквивалентная абсолютная шероховатость.

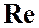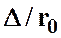Третья область ─ область больших и , где 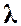не зависит от числа 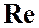, а определяется лишь относительной шероховатостью (область расположена справа от пунктирной линии). Это область шероховатых труб, в которой все линии с различными шероховатостями параллельны между собой. Эту область называют областью автомодельности или режимом квадратичного сопротивления, так как здесь гидравлические потери пропорциональны квадрату скорости.

Определение 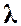для этой области производят по упрощенной формуле Альтшуля

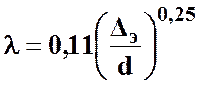. (3.21)