Выпуклые функции и точки перегиба
Пусть функция  определена на
определена на 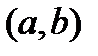 .
.
Определение 2. Говорят, что  является выпуклой вниз функцией на
является выпуклой вниз функцией на 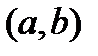 , если для любых двух точек
, если для любых двух точек 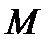 и
и 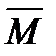 , которые принадлежат графику функции
, которые принадлежат графику функции  , дуга, которая соединяет эти точки, лежит под хордой
, дуга, которая соединяет эти точки, лежит под хордой 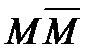 (рис.3).
(рис.3).
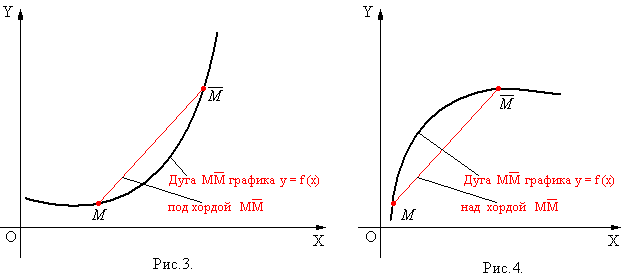
Определение 3. Говорят, что  является выпуклой вверх функцией на
является выпуклой вверх функцией на 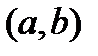 , если для любых двух точек
, если для любых двух точек 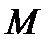 и
и 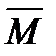 , которые принадлежат графику функции
, которые принадлежат графику функции  , дуга, которая соединяет эти точки, лежит над хордой
, дуга, которая соединяет эти точки, лежит над хордой 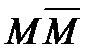 (рис.4).
(рис.4).
Теорема 4. Пусть функция  определена и дифференцирована на
определена и дифференцирована на 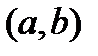 . Для того, чтобы
. Для того, чтобы  была выпуклой вниз (вверх) на
была выпуклой вниз (вверх) на 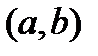 необходимо и достаточно, чтобы производная
необходимо и достаточно, чтобы производная 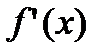 монотонно возрастала (убывала) (не обязательно строго) на
монотонно возрастала (убывала) (не обязательно строго) на 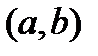 .
.
Следствие. Пусть функция  определена и дважды дифференцирована на
определена и дважды дифференцирована на 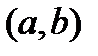 . Для того, чтобы
. Для того, чтобы  была выпуклой вниз (вверх) на
была выпуклой вниз (вверх) на 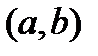 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
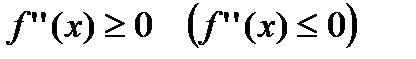 для
для 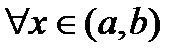 .
.
Определение 4. Пусть функция  определена на
определена на 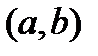 и точка
и точка 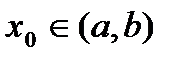 . Пусть существует окрестность точки
. Пусть существует окрестность точки 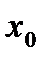 такая, что слева и справа от точки
такая, что слева и справа от точки 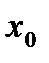 в этой окрестности функция
в этой окрестности функция  сохраняет направление выпуклости. Если эти направления разные, то точка
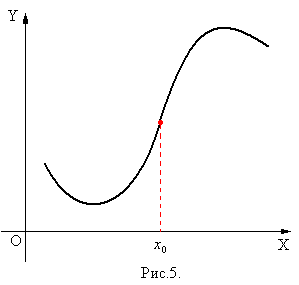
сохраняет направление выпуклости. Если эти направления разные, то точка 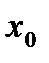 называется точкой перегиба функции (рис.5).
называется точкой перегиба функции (рис.5).
Теорема 5 (необходимое условие точки перегиба функции). Пусть функция  определена на
определена на 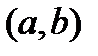 . Если точка
. Если точка 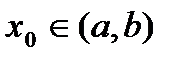 является точкой перегиба для функции
является точкой перегиба для функции  , то выполняется одно из следующих условий:
, то выполняется одно из следующих условий:
- 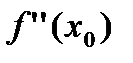 не существует;
не существует;
- 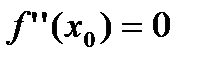 .
.
Таким образом, точки, подозрительные на перегиб, - это точки из 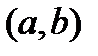 , где производная второго порядка не существует или равняется нулю.
, где производная второго порядка не существует или равняется нулю.
Теорема 6 (достаточное условие точки перегиба функции). Пусть функция  определена, дважды дифференцирована на
определена, дважды дифференцирована на 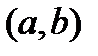 и
и 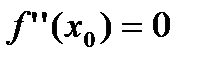 . Если
. Если  имеет производную третьего порядка в точке
имеет производную третьего порядка в точке 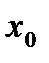 и
и 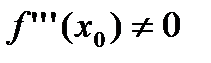 , то точка
, то точка 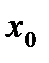 является точкой перегиба для функции
является точкой перегиба для функции  .
.
Пример. Найти точки перегиба функции 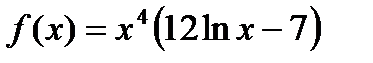 . Область определения функции:
. Область определения функции: 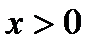 . Сначала надо найти точки, которые являются подозрительными на перегиб. Для этого найдем производную второго порядка:
. Сначала надо найти точки, которые являются подозрительными на перегиб. Для этого найдем производную второго порядка:
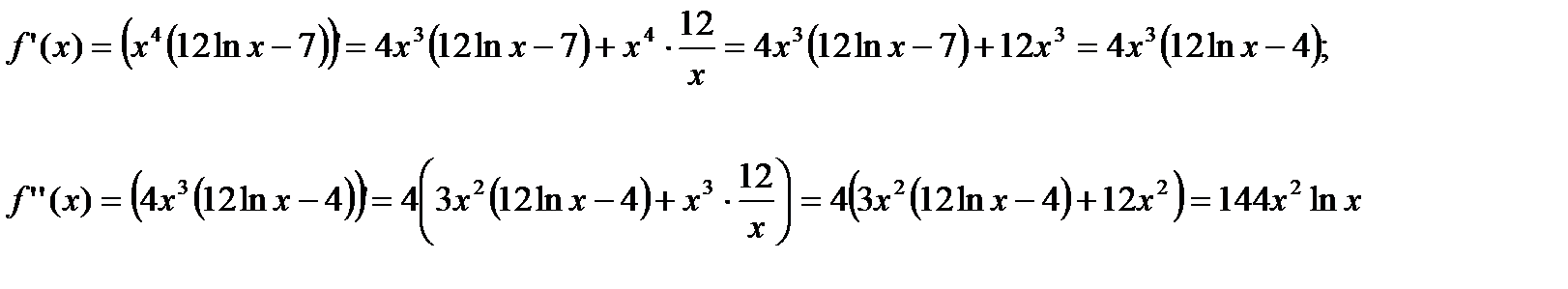
На области определения функции нет точек, где 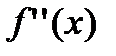 не существует. Найдем нули для
не существует. Найдем нули для 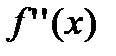 :
:
 .
.
На области определения функции 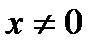 , поэтому ноль
, поэтому ноль 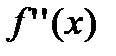 определится только благодаря
определится только благодаря  . Таким образом,
. Таким образом, 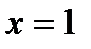 - единственная точка, подозрительная на перегиб. Эта точка разделяет область определения функции на два множества, где
- единственная точка, подозрительная на перегиб. Эта точка разделяет область определения функции на два множества, где 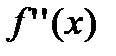 сохраняет свой знак, а потому
сохраняет свой знак, а потому  сохраняет характер выпуклости (см. табл.1).
сохраняет характер выпуклости (см. табл.1).
Таблица 1 –

Вопросы
1. Какие точки называются стационарными для функции  ?
?
2. Как определить точки, подозрительные на экстремум для функции  ? Необходимое условие локального экстремума функции.
? Необходимое условие локального экстремума функции.
3. Всегда ли для нахождения экстремума функции можно пользоваться первым достаточным условием?
4. Второе достаточное условие локального экстремума.
5. Третье достаточное условие локального экстремума.
6. Для любой ли функции можно найти ее наименьшее и наибольшее значения?
7. Определение выпуклой вниз (вверх) функции.
8. Критерий выпуклости функции.
9. Определение точки перегиба функции. Необходимое условие точки перегиба функции.
10. Достаточное условие точки перегиба функции.
Дата добавления: 2015-08-21; просмотров: 1003;
