Понятие дифференциала функции
Пусть функция  определена на
определена на 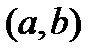 ,
,  ,
,  дифференцируема в точке
дифференцируема в точке 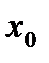 , т.е. в окрестности точки
, т.е. в окрестности точки 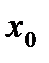 представляется согласно (5):
представляется согласно (5):
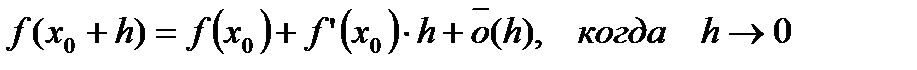 .
.
Разность 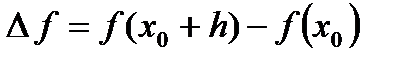 называется приращением функции в точке
называется приращением функции в точке  , а
, а  приращением аргумента. В принятых обозначениях предыдущая формула будет иметь вид:
приращением аргумента. В принятых обозначениях предыдущая формула будет иметь вид:
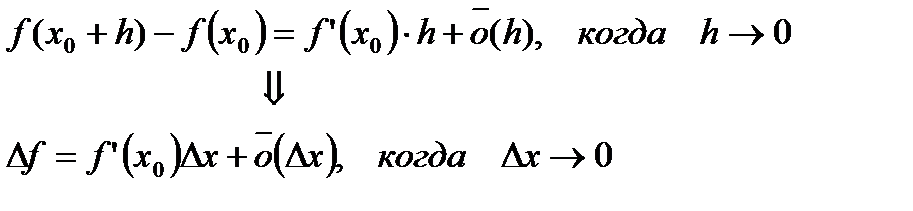
Определение 5. Дифференциалом функции  в точке
в точке 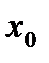 называется линейная функция
называется линейная функция
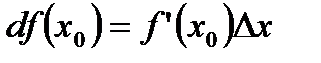 .
.
Дифференциал - это линейная часть приращения функции. Дифференциал функции сам является функцией.
Приращение аргумента 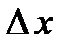 также называют дифференциалом независимой переменной
также называют дифференциалом независимой переменной 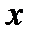 и обозначают:
и обозначают:
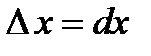 .
.
Тогда
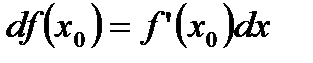 .
.
Пример. Найти дифференциал функции 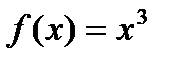 в произвольной точке
в произвольной точке 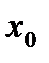 . Для этого надо:
. Для этого надо:
1. Найти выражение для приращения функции в точке 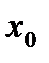 ;
;
2. В выражении для приращения функции в точке 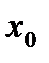 найти линейную часть, т.е. ту часть, которая содержит
найти линейную часть, т.е. ту часть, которая содержит 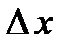 в первой степени;
в первой степени;
3. Для той части приращения функции, которая осталась после выделения линейной части, доказать, что она является бесконечно малой, порядка высшего, чем 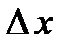 , когда
, когда 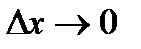 ;
;
4. Если третий шаг выполнен, то линейная часть приращения функции, найденная на втором шаге, и является дифференциалом функции в точке 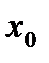 .
.
Проделаем последовательно действия всех четырех шагов для функции 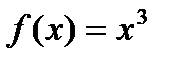 :
:
1. 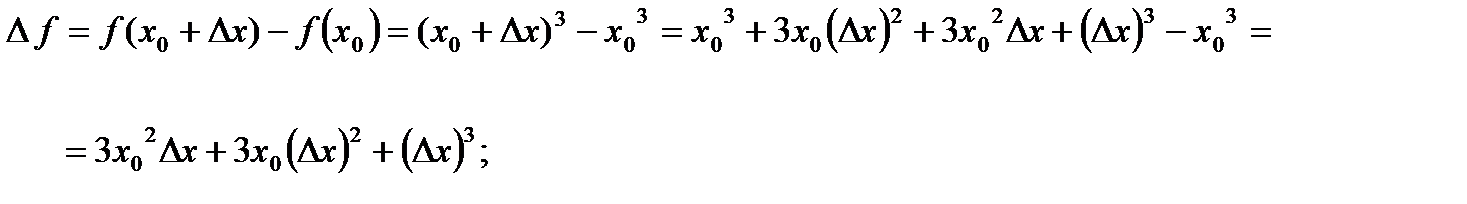
2. Линейная часть полученного приращения функции 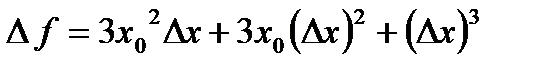 - это
- это 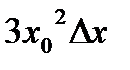 . В этом слагаемом
. В этом слагаемом 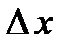 находится в первой степени, а в других слагаемых -
находится в первой степени, а в других слагаемых -  и
и 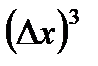 показатели степени при
показатели степени при 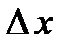 соответственно 2 и 3.
соответственно 2 и 3.
3. После выделения линейной части приращения осталось: 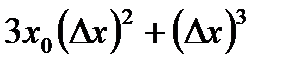 . Проверим, что
. Проверим, что 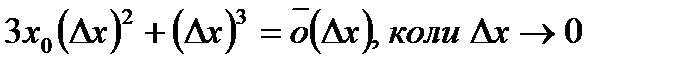 . Для этого вычислим:
. Для этого вычислим:
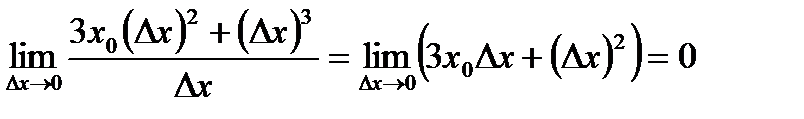 .
.
Поскольку вычисленный предел равняется 0, то действительно 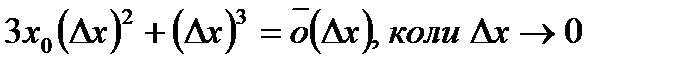 .
.
Таким образом
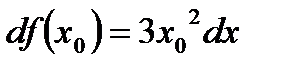 .
.
Дата добавления: 2015-08-21; просмотров: 666;
