Изображение синусоидальных ЭДС, напряжений и токов на плоскости декартовых координат
// Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е1ие2соответствуют уравнения:
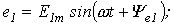
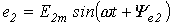 .
.
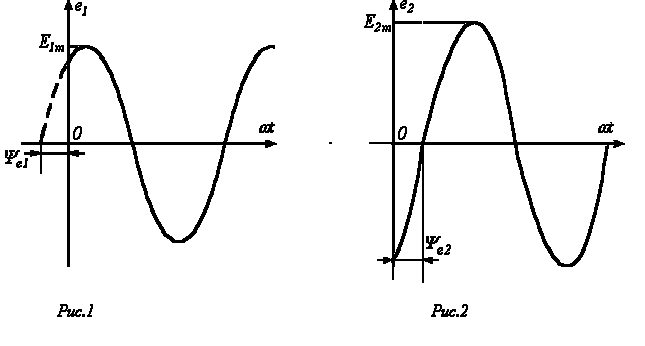
Значения аргументов синусоидальных функций 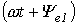 и
и 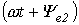 называются фазамисинусоид, а значение фазы в начальный момент времени (t=0):
называются фазамисинусоид, а значение фазы в начальный момент времени (t=0): 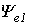 и
и 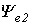 - начальной фазой(
- начальной фазой( 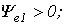
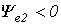 ).
).
Величину 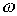 , характеризующую скорость изменения фазового угла, называют угловой частотой.Так как фазовый угол синусоиды за время одного периода Т изменяется на
, характеризующую скорость изменения фазового угла, называют угловой частотой.Так как фазовый угол синусоиды за время одного периода Т изменяется на 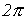 рад., то угловая частота есть
рад., то угловая частота есть 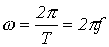 , где f– частота.
, где f– частота.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.
Для синусоидальных ЭДС е1ие2угол сдвига фаз:
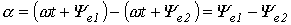 .
.
Дата добавления: 2015-08-20; просмотров: 623;
