Числовые множества

Множество N={1,2,3,…} – называют множеством натуральных чисел.

Однако, уравнение x + 1 = 0 не имеет решения в этом множестве. Пришлось это множество расширять.

Множество Z={…,-2,-1,0,1,2,…} – называют множеством целых чисел.

Однако уравнение 2x+3=0 не имеет решения в этом множестве.

Множество Q={p/q}, где p Z, q Z, q≠0 – называют множеством рациональных чисел.

Однако, уравнение x² – 3 = 0 не имеет решений в этом множестве.

Множество R – множество действительных чисел (вещественных чисел – чисел рациональных и иррациональных).

Однако, уравнение x² + 2 = 0 не имеет решений в этом множестве.

Множество С ={x+iy} – называется множеством комплексных чисел, если x R, y R, 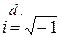– «мнимая» единица.

Очевидно, что .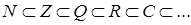

1.3. Декартова прямоугольная система координат[2]

 

Def.	Декартова прямоугольная система координат (д.п.с.к.) на плоскости – две взаимно перпендикулярные прямые с выбранным масштабом и направлением (оси).

 

Обычно д.п.с.к. обозначают X0Y.

 

Если т. M(x;y) – принадлежит плоскости с д.с.п.к. X0Y, то x - называют абсциссой, y – ординатой.

 

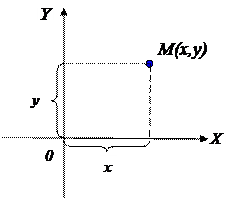В трехмерном пространстве д.п.с.к. XYZ – три взаимно перпендикулярные прямые (пересекающиеся в одной точке) с выбранным масштабом и направлением (оси).

Если т. M(x;y;z) – принадлежит трехмерному пространству с д.с.п.к. XYZ, то x – называют абсциссой, y – ординатой, z – аппликатой.