ГЛАВА 1. Элементы теории множеств. Системы координат
Основные понятия о множествах
Множеством называют совокупность элементов, обладающих общим признаком.
Множество – понятие первичное и через более простое не определяется.
Множество можно заменить словами – «совокупность», «класс», «объединение» и т.д.
Пусть А – произвольное множество. Если элемент а содержится (не содержится) во множестве А, то записывают 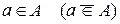 .
.
Пусть В – другое множество.
Обозначим:
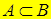
| – содержание А в В (включение А в В, …); |

| – совпадение А и В (равенство А и В, …); |

| – пересечение А и В (умножение А∙В, …); |

| – объединение А и В (сумма А и В, …); |
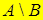
| – дополнение В до А (разность А и В, …); |

| – декартово произведение А и В (прямое произведение А и В,
т.е. множество пар (а; b), где 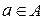 , , 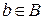 , …); , …);
|
| Ø | – пустое множество; |

| – мощность множества А (если А – конечное множество,
то 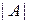 – число его элементов, …). – число его элементов, …).
|
Геометрически – множества можно изобразить с помощью диаграмм Эйлера-Венна[1].
На этих диаграммах множества изображают точками кругов, прямоугольников, треугольников и т.д.
Например, для пересекающихся множеств А и В мы можем изобразить диаграмму Эйлера-Венна.
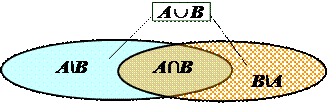 |
Дата добавления: 2015-08-20; просмотров: 691;
