Жидкостная экстракция
Принцип экстракции в системе жидкость – жидкость основан на различной растворимости распределяемого компонента в распределяющих веществах.
Жидкостная экстракция находит широкое применение в различных отраслях промышленности: при производстве технологических органических веществ и редких металлов, очистке продуктов и полупродуктов от примесей, получении ядерного горючего, синтезе лекарственных веществ, а также в радиационной химии, процессах нефтепереработки и нефтехимии.
Благодаря простоте осуществления, низким энергетическим затратами высокой эффективности процессы жидкостной экстракции успешно конкурируют, а иногда используются в сочетании с другими процессами разделения (ректификацией, выпариванием и др.). Ею можно разделять азеотропные смеси, а также смеси компонентов с близкими температурами кипения и малой относительной летучестью.
В процессе жидкостной экстракции исходная смесь F, содержащая распределяемое вещество, вступает в контакт с экстрагентом (растворителем) S, в который в результате массопередачи переходит компонент. После разделения (отстаивание, центрифугирование или другой метод) получают две новые фазы – экстракт Е, представляющий собой раствор распределяемого вещества в экстрагенте, и рафинат R – исходный раствор, из которого частично или полностью извлечено распределяемое вещество.
В ряде случаев следующей стадией за процессом экстракции и разделения полученных продуктов является регенерация экстрагента (удаление из экстракта ранее поглощенного компонента), которую можно осуществить ректификацией, перегонкой в токе водяного пара, повторной экстракцией, реже кристаллизацией или химической обработкой.
При выборе экстрагента (растворителя) к его составу предъявляют ряд требований: селективность (избирательность) по отношению к извлекаемому компоненту; высокая растворимость извлекаемого компонента; возможность проведения эффективной регенерации; разность плотностей с исходной смесью, достаточной для расслоения полученных продуктов; безопасность при работе (отсутствие токсичности, пожаро- и взрывобезопасность); сохранение свойств при обработке, хранении, регенерации; низкая стоимость; доступность.
Основные промышленные экстрагенты, применяемые в процессах экстракции, делятся на три класса.
1. Органические кислоты или их соли (алифатические монокарбоновые кислоты, нафтеновые кислоты, сульфокислоты, фенолы, оксимы, кислые эфиры фосфорной кислоты), которые извлекают катионы металлов в органическую фазу из водной.
2. Соли органических оснований (соли первичных, вторичных и третичных аминов, а также четвертичных аммониевых оснований), с помощью которых извлекают анионы металлов из водных растворов.
3. Нейтральные растворители (вода, спирты, простые и сложные эфиры, альдегиды и кетоны), с помощью которых осуществляют разные механизмы извлечения в зависимости от кислотности исходного раствора.
Равновесие в процессах жидкостной экстракции подчиняется так называемому закону распределения. В соответствии с этим законом отношение равновесных концентраций распределенного между двумя жидкими фазами вещества при постоянной температуре есть величина постоянная, называемая коэффициентом распределения
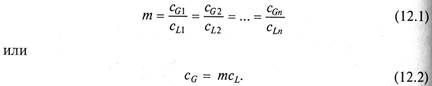
В уравнениях (12.1) и (12.2) размерность концентраций выражена в кг/м3.
Если уравнения (12.1) и (12.2) записать для соответствующих, концентраций (у, х), размерности которых выражаются в кг/кг растворителя, они примут вид
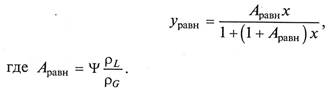
По величине коэффициента распределения судят об экстракционной способности экстрагента. Так, увеличение значения Ψ соответствует более высокой способности экстрагента извлекать целевой компонент. Значение коэффициента распределения находится в пределах от 1 до 10000.
Коэффициент распределения зависит от свойств взаимодействующих систем, наличия химического взаимодействия извлекаемого компонента с растворителем. Величина т незначительно зависит от температуры и, вследствие несжимаемости жидкостей, практически не зависит от давления.
Данные для построения линий равновесия и значения коэффициентов распределения приведены в справочниках.
При рассмотрении статики процесса экстракции предполагалось, что экстрагент и раствор, содержащий распределяемый компонент, являются взаимно нерастворимыми или же обладают незначительной растворимостью.
Если же они взаимно растворимы, то для таких систем равновесные соотношения изображаются с помощью треугольных диаграмм, построенных для постоянной температуры.
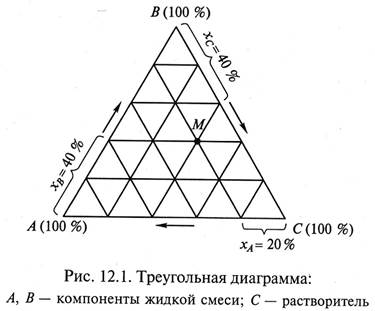
Треугольная диаграмма (рис. 12.1) представляет собой равносторонний треугольник, вершины которого соответствуют содержанию чистых компонентов А, В и С. При этом А и В – компоненты жидкой смеси, подлежащей разделению, С – растворитель. Стороны треугольника являются шкалами, точки которых определяют составы двухкомпонентных смесей или растворов АВ (компонента В), СА (компонента А) и ВС (компонента С), а точки внутри треугольника – составы трехкомпонентных систем.
Так, точка М на рис. 12.1 соответствует составу тройной смеси, содержащей 20% компонента А, 40% компонента В и 40% компонента С.
В дальнейшем, считая, что исходная смесь и экстрагент взаимно нерастворимы, для изображения процессов экстракции будем использовать диаграмму у – х.
Материальный баланс процесса экстракции соответствует общему для массообменных процессов уравнению
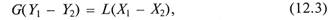
где G – количество экстрагента; L – количество исходного растворителя; Y1 и Y2 – содержание распределяемого компонента в экстракте и экстрагенте, кг компонента/кг экстрагента; Х1 и Х2 –содержание распределяемого компонента в исходном растворе и рафинате, кг компонента/кг исходного растворителя.
Из уравнения (12.3) можно определить необходимый расход экстрагента
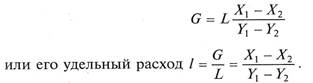
Зависимость между составами экстрагента и рафината графически выражается рабочей линией, являющейся прямой, уравнение которой соответствует уравнениям (9.4) и (9.5), крайние точки которой определяются составами исходного раствора, экстрагента, экстракта и рафината.
Процессы экстракции проводятся чаще всего без подвода или отвода теплоты, поэтому для их расчета составление теплового баланса не требуется.
Уравнение материального баланса может быть записано для процесса экстракции по входящими выходящим потокам в виде
F+S=R+E,
где F, S, R, Е – весовые расходы исходного раствора, экстрагента, рафината и экстракта.
Кинетика процесса экстракции (кинетические закономерности) определяются основными законами массопередачи. В процессе происходит взаимодействие капель дисперсной фазы и дисперсионной среды. При этом основными стадиями этого процесса являются: переход распределяемого вещества из среды к поверхности капли, а затем внутрь нее или, наоборот, из капли через поверхность раздела фаз в ядро потока среды.
При этом различают три случая.
1. Диффузионное сопротивление сосредоточено в дисперсионной среде.
В этом случае коэффициент массопередачи Кх может быть принят равным коэффициенту массоотдачи среды βс, т. е. Кх ≈ βс, а количество переданного вещества определяется из соотношения
М = βс*Δхср*F
Коэффициент массоотдачи для этого случая рассчитывается по критериальному уравнению
Nuдиф.с = βс*d/Dдиф.с = f*(Peдиф.с),
где Nuдиф.с – диффузионный критерий Нуссельта для среды; Dдиф.с – коэффициент диффузии распределяемого вещества в среде; d — диаметр капли; Peдиф.с = wd/Dдиф.с - диффузионное число Пекле для среды; w —относительная скорость движения капли и
среды.
2. Диффузионное сопротивление сосредоточено в дисперсной фазе (капля).
Коэффициент массопередачи Ку может быть принят равным коэффициенту массоотдачи дисперсной фазы βдисп, т. е. Ку≈ βдисп, а количество переданного вещества определяется из соотношения
М = βдисп*Δуср* F
Коэффициент массоотдачи для этого случая определяется из уравнения
Nuдиф.д = βс*d/Dдиф.д = f*(Peдиф.д),
где Nuдиф.д – диффузионный критерий Нуссельта для дисперсной фазы; Dдиф.д – коэффициент диффузии распределяемого вещества в капле; Peдиф.д = wd/Dдиф.д – диффузионное число Пекле для капли.
Диффузионные сопротивления в среде и капле соизмеримы.
В этом случае количество переданного вещества определяется в соответствии с основным уравнением массопередачи (9.7), а коэффициенты массопередачи рассчитываются по выражениям
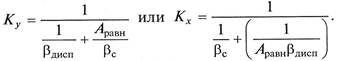
Дата добавления: 2015-08-14; просмотров: 2684;
