Переменная емкость

Емкость 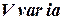представлена на рис. 10.6. в виде пространства, к которому подвод и отвод жидкости регулируются распределительными органами 1 и 2 и которые ограничено с одной стороны поршнем 3. Для координат сохраняем обозначения, которыми отмечены соответствующие элементы динамической системы. Уравнение емкости запишем в таком виде:

.

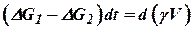(10.27)

Правую часть (10.27) разделим на два слагаемых:

,

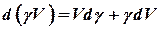где 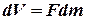, 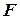- активная площадь поршня.

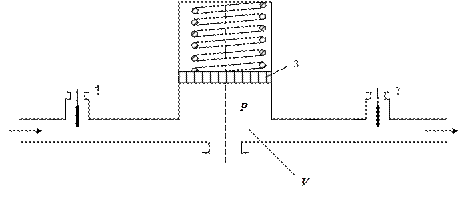
Рисунок 7.6 – Схема аккумулятора газа с переменным объемом

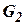Выполнив разложение функций и в степенной ряд, вместо (10.27) получим:

,

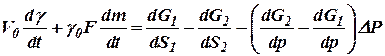(10.28)

где 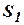, 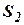и – координаты соответственно распределительных органов и поршня.

Если массой поршня пренебречь, можно установить алгебраическую связь между его ходом и изменением давления ,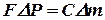

где 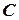– жесткость пружины. Согласно последнему уравнению и соотношениям п.2.1, получим

.

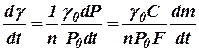Выразив 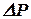через 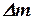и поделив все члены уравнения (10.28) на величину 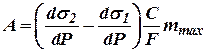, представим уравнение емкости в виде:

,

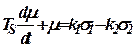(10.29)

где

; ; .

,

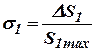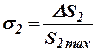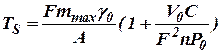(10.30)

где

; .

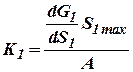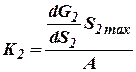Величина 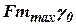представляет собой весовое количество жидкости, вытесняемой или всасываемой поршнем в течение его максимального хода. Величина 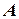характеризует изменение расхода жидкости под влиянием изменения давления 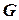пределах 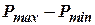при неизменном положении распределительных органов. Дробь, стоящая перед скобкой 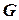(10.30), характеризует относительную величину максимального объема жидкости, вытесняемого поршнем, по сравнению с изменением ее расхода в указанных условиях.

Второй член в скобках (10.30) отражает влияние на процесс регулирования сжимаемости жидкости. 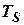имеет размерность времени.