Постоянная емкость
Представим себе резервуар неизменной вместимости V, заполненный газом, который принимает в резервуар в единицу времени в количестве  и в то же время вытекает из него в количестве
и в то же время вытекает из него в количестве  (рис.10.5).
(рис.10.5).
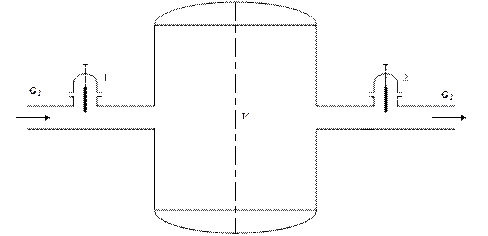
Рисунок 10.5 – Схема аккумулятора газа с постоянным объемом
На эти расходы газа можно влиять посредством задвижек 1 и 2. При установившемся движении газа
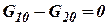
| (10.16) |
Путем воздействия на распределительные органы нарушим равенство расходов (10.16). Тогда согласно закону сохранения материи
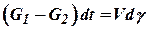 , ,
| (10.17) |
где 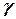 - удельный вес газа
- удельный вес газа
Разделив обе части (10.17) на 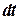 и вычитая получено (10.16) из (10.17), получим:
и вычитая получено (10.16) из (10.17), получим:
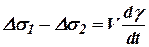 , ,
| (10.18) |
где 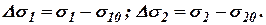
Выберем в качестве параметра, характеризующего состояние газа в аккумуляторе, давление 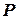 . Предположим, что во время неустановившегося процесса состояние газа в резервуаре изменяется политропно, то есть:
. Предположим, что во время неустановившегося процесса состояние газа в резервуаре изменяется политропно, то есть:
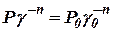 , ,
| (10.19) |
где n- показатель политропы.
После дифференцирования (10.19) найдем:
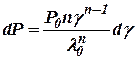 . .
| (10.19) |
В уравнение (10.20) левую и правую часть разделим на 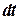 , подставим
, подставим 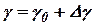 и разложим в ряд (бином Ньютона) выражение:
и разложим в ряд (бином Ньютона) выражение:
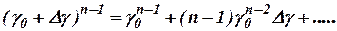
Тогда 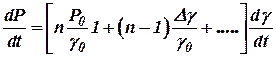 .
.
Рассматривая колебания малыми, считаем что 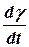 величина малая, а произведение
величина малая, а произведение 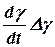 величиной второго порядка малости. Поэтому, отбросив величины второго и высшего порядка малости, последнее уравнение запишем так:
величиной второго порядка малости. Поэтому, отбросив величины второго и высшего порядка малости, последнее уравнение запишем так:
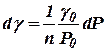 . .
| (10.21) |
В (10.18) введем 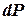 вместе
вместе 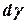 и обозначим D0вес газа в данном резервуаре, т.е. положим
и обозначим D0вес газа в данном резервуаре, т.е. положим 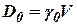 .
.
Тогда
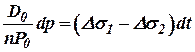 . .
| (10.22) |
Предположим, что расходы газа G1 и G2 можно представить в виде следующих функций:
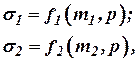
где 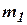 и
и 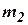 –координаты, определяющие положения распределительных органов 1 и 2 (рис.10.5). При этом давление до задвижки 1 и после задвижки 2 считаем неизменным. Тогда для малых колебаний имеем:
–координаты, определяющие положения распределительных органов 1 и 2 (рис.10.5). При этом давление до задвижки 1 и после задвижки 2 считаем неизменным. Тогда для малых колебаний имеем:
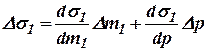 , ,
| (10.23) |
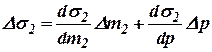 . .
| (10.24) |
Подставив (10.23) и (10.24) в (10.22) и представив переменные в относительных единицах, получим уравнение газового объема в форме:
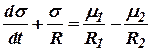 , ,
| (10.25) |
где
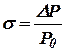 ;
; 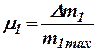 ;
; 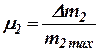 ;
; 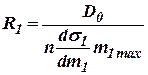 ;
; 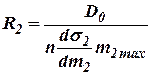 ;
; 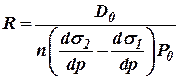 .
.
Динамическая постоянная  имеет положительное значение так как
имеет положительное значение так как 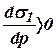 и
и 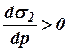 .
.
Динамические постоянные 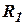 ,
, 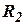 и
и  имеют размерность времени и называются временами емкости.
имеют размерность времени и называются временами емкости.
Количество газа, поступающего в резервуар и вытекающего из него, может зависеть от дополнительных параметров по сравнению с принятыми в уравнениях (10.23) и (10.24). Так, например, давление перед задвижкой 1 может изменятся 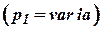 , а тогда
, а тогда 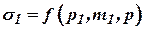 .
.
В этом случае в уравнении емкости появится дополнительный член с переменной Р1.
Допустим, что во всем диапазоне изменений расход G1 линейно зависит от координаты m1. Тогда при n=1 константа 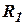 приобретает смысл времени заполнения объема
приобретает смысл времени заполнения объема 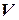 при полностью открытой задвижки 1 и закрытой задвижки 2, если во время заполнения расход условно считать неизменным и равным расходу для давления
при полностью открытой задвижки 1 и закрытой задвижки 2, если во время заполнения расход условно считать неизменным и равным расходу для давления  установившегося режима. Аналогичное условное толкование можно дать константе
установившегося режима. Аналогичное условное толкование можно дать константе 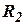 .
.
Так же как для ротора в предыдущем параграфе, умножим обе части уравнения (10.25) на R и запишем это уравнение в операторной форме:
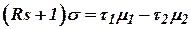 или или 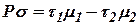
| (10.26) |
где 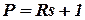 ;
; 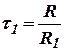 ;
; 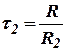 .
.
Коэффициенты 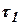 и
и 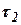 не содержат емкости и носят статический характер.
не содержат емкости и носят статический характер.
Дата добавления: 2015-08-14; просмотров: 806;
