Порядковый (ординалистский) подход

Порядковый подход к анализу полезности и спроса является более современным и основывается на гораздо менее жестких предположениях, чем количественный подход. От потребителя не требуется умения измерять полезность того или иного блага в каких-то искусственных единицах измерения. Достаточно лишь, чтобы потребитель был способен упорядочить все возможные товарные наборы по их "предпочтительности".

Порядковый подход базируется на следующих аксиомах.

1. Аксиома полной (совершенной) упорядоченности. Потребитель способен упорядочить все возможные наборы товаров с помощью отношений предпочтения (у) и безразличия (~). Это означает, что для любой пары товарных наборов А и В потребитель может указать, что либо А > В (А предпочтительнее, чем В), либо В > А (В предпочтительнее, чем А), либо А ~ В (А и В равноценны).

Обратим внимание на то, что символы А и В здесь обозначают не отдельные товары, а товарные наборы.

Очевидно, что данная аксиома не является слишком жесткой. Она лишь исключает возможность ответа "не знаю" на вопрос: "Какой из этих двух товарных наборов Вы предпочитаете?". Потребитель может выбрать любой из них либо сказать, что оба представляют для него одинаковую ценность.

2. Аксиома транзитивности. Если А > В > С, или А ~ В> С, или А > В ~ С, то А > С. Эта

аксиома гарантирует согласованность предпочтений. Она, например, исключает возможность следующей ситуации: А > В, В > С и одновременно С > А.

Аксиома транзитивности содержит и еще одно утверждение, а именно: если А ~ В и В ~ С, то А ~ С. Однако интерпретация ее сопряжена с известными сложностями. Пусть, например, индивидууму безразлично, положить в стакан чая 6 или 7 г сахарного песку, 7 или 8 г и т.д. Но тогда в силу только что высказанного утверждения ему должно быть безразлично, положить ли в него 6 или, скажем, 100 г сахара, что маловероятно. Парадокс объясняется наличием определенного порога восприятия.1 Для устранения его может потребоваться привести единицу измерения в соответствие с порогом восприятия (например, измерять песок не граммами, а чайными ложечками).

3. Аксиома ненасыщения. Если набор А содержит не меньшее количество каждого товара, а одного из них больше, чем набор В, то А > В. Таким образом, предполагается, что увеличение потребления любого товара - при фиксированных объемах потребления других товаров - улучшает положение потребителя.

В принципе теорию потребительского выбора можно построить и без этой аксиомы. Но она значительно упрощает все последующие рассуждения.

4. Аксиома независимости потребителя. Удовлетворение потребителя зависит только от количества потребляемых им благ и не зависит от количества благ, потребляемых другими.

Это, прежде всего, означает, что потребителю не знакомы чувства зависти и сострадания. В принципе и от этой аксиомы можно отказаться, что иногда и делается, в частности при анализе процессов потребления, сопровождающихся внешними эффектами и внешними затратами.

В порядковой теории полезности понятие "полезность" означает не более чем порядок предпочтения. Утверждение "Набор А предпочтительнее набора B" эквивалентно утверждению "Набор А имеет большую для данного потребителя полезность, чем набор В". Вопрос о том, на сколько каких-либо единиц полезности или во сколько раз набор А предпочтительнее (или имеет большую полезность), чем набор В, не ставится. Таким образом, задача максимизации полезности сводится к задаче выбора потребителем наиболее предпочтительного товарного набора из всех доступных для него.

Закон предельной полезности.

Закон уменьшения предельной полезности – чем больше вы потребляете какого-либо блага (товара), тем меньше дополнительной полезности приносит вам потребление каждой дополнительной единицы этого блага (товара). Есть также мнение, что иногда бывают случаи, когда дополнительная единица товара может принести больше удовлетворения, чем предыдущая, но это бывает редко и недолго – после некоторого уровня насыщения закон уменьшения предельной полезности выполняется всегда и неукоснительно.

Правило максимизации полезности – рациональный потребитель всегда выберет тот вариант, при котором он получит больше полезности.

Кривые безразличия и их свойства.

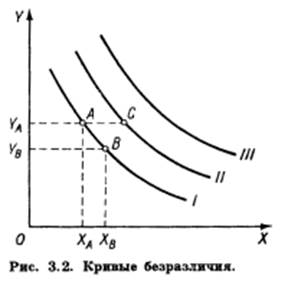При порядковом подходе используются кривые и карта безразличия. Кривая безразличия - это множество точек, каждая из которых представляет собой такой набор из двух товаров, что потребителю безразлично, какой из этих наборов выбрать. Если заполнить двухмерную плоскость кривыми безразличия так плотно, как это возможно, получим карту безразличия.

На рис. 3.2 товарный набор А включает ХА единиц товара X и YА единиц товара Y, товарный набор В включает ХB единиц товара X и YB единиц товара Y. Если с точки зрения данного потребителя наборы А и В равноценны, то точки А и В лежат на одной и той же кривой безразличия.

Кривые безразличия обладают следующими свойствами.

А. Кривая безразличия, лежащая выше и правее другой кривой, представляет собой более предпочтительные для данного потребителя наборы товаров.

Б. Кривые безразличия имеют отрицательный наклон

В. Кривые безразличия никогда не пересекаются.

Г. Кривая безразличия может быть проведена через любую точку пространства товаров. Говорят еще, что кривая безразличия не имеет "толщины". Это свойство любых линий в Евклидовой геометрии, оно является, безусловно, определенной идеализацией, абстракцией реального мира. Чтобы сделать его более реалистичным, необходимо при выборе единицы измерения товаров учитывать порог восприятия.

Д. Кривые безразличия выпуклы к началу координат.

Взаимозаменяемость экономических благ. Предельная норма замещения.

Основным рабочим понятием порядковой теории полезности является предельная норма замещения (MRS; marginal rate of substitution - англ.).

Предельной нормой замещения благом X блага Y(MRSXY) называют количество блага Y, которое должно быть сокращено "в обмен" на увеличение количества блага X на единицу, с тем, чтобы уровень удовлетворения потребителя остался неизменным.

Предельная норма замещения может принимать различные значения, она может быть равна нулю, может быть неизменной или меняться при движении вдоль кривой безразличия. В случае выпуклости к началу координат, как на рис. 3.5, MRS убывает по мере замещения одного блага другим, т.е. потребитель соглашается отдавать все меньшее количество замещаемого блага за одно и то же количество замещающего (аналог убывающей предельной полезности).

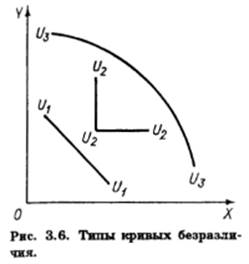
Для двух совершенно взаимозаменяемых товаров MRS = const. В этом случае кривые безразличия вырождаются в прямые линии (линия U1U1 на рис. 3.6). Обычно такие товары рассматриваются как один товар.

Возможно, далее, что товары вообще не могут заменять друг друга, как, например, правый и левый ботинок. Потребитель получит одно и то же удовлетворение, имея один левый и два правых ботинка, как и имея, наоборот, два левых и один правый. Такие товары жестко дополняют друг друга. В этом случае каждая кривая безразличия вырождается в два взаимно перпендикулярных отрезка (U2U2 на рис. 3.6). Наконец, иногда возможно, что, чем больше какого-то товара имеет потребитель, тем больше

он хотел бы иметь его. В этом случае кривая безразличия вогнута к началу координат, и норма замещения возрастает (U3U3 на рис. 3.6). Хотя ни один из этих вариантов не может быть исключен, выпуклость кривых безразличия и убывающая норма замещения представляют наиболее общую и распространенную ситуацию.

Бюджетные ограничения потребителя.

Карта безразличия представляет собой графическое отображение системы предпочтений потребителя. Естественно, потребитель стремится приобрести товарный набор, принадлежащий наиболее удаленной от начала координат кривой безразличия. Но он ограничен в своих средствах. Далеко не всякий товарный набор ему доступен. Для изображения множества доступных потребителю товарных наборов используется бюджетная линия.

Обозначим месячный доход потребителя через I. Для упрощения предположим, что потребитель не делает никаких сбережений и весь свой доход расходует на приобретение только двух товаров X и Y. Бюджетное ограничение потребителя можно записать в форме следующего равенства:

I = PX + PY

Бюджетное ограничение имеет очевидный смысл: доход потребителя равен сумме его расходов на покупку товаров X и У. Преобразуем равенство (3.10) к следующему виду:

Y= I/РX +I/ PY

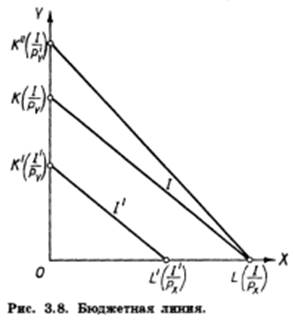
Мы получили уравнение бюджетной линии, или, как ее еще называют, линии цен. На рис. 3.8 эта линия первоначально занимает положение KL.

Точки пересечения бюджетной линии с осями координат можно получить следующим образом. Если потребитель весь свой доход / израсходует только на покупку товара X, то он сможет приобрести I/PX единиц этого товара. Поэтому длина отрезка OL равна I/PX. Аналогично можно показать, что длина отрезка ОК равна 1/РY. Наклон бюджетной линии равен ≈РX/РY ≈ коэффициенту при X в уравнении (3.11).

Все товарные наборы, соответствующие точкам на бюджетной линии, стоят ровно I руб. и являются потому доступными для нашего потребителя. Все товарные наборы, расположенные выше и правее бюджетной линии, стоят более I руб. и недоступны для потребителя. Таким образом, бюджетная линия ограничивает сверху множество доступных для потребителя товарных наборов.

Как изменится положение бюджетной линии при изменении дохода потребителя и цен на товары? Допустим сначала, что доход потребителя уменьшается до I` < I, цены на товары при этом остаются неизменными. Наклон бюджетной линии не изменится, поскольку он определяется только соотношением цен. Следовательно, произойдет параллельный сдвиг бюджетной линии вниз. Она займет положение К'L'. При увеличении дохода и неизменных ценах будет наблюдаться параллельный сдвиг бюджетной линии вверх. Предположим теперь, что доход и цена товара X неизменны, цена же товара Y понизилась до Р`Y < РY. Очевидно, что в этом случае точка L не изменит своего положения, поскольку оно определяется неизменными I и РX. Левый же конец бюджетной линии сдвинется вверх и займет положение К". Читатель может без труда определить, что случится с бюджетной линией при повышении РY, повышении или понижении РX.

Равновесие в потреблении.

Потребительское равновесие – ситуация, в которой потребитель не может увеличить общую полезность, получаемую исходя из данного бюджета, расходуя меньше денег на покупку одного блага и больше на покупку другого блага.

Итальянский экономист Парето доказал, что максимальная эффективность потребления достигается в том случае, когда предельная полезность всех приобретаемых товаров в расчёте на единицу вложенных средств одинакова. То есть когда предельная полезность блага А поделить на цену блага А равна предельной полезности блага Б поделить на цену Б и равна предельной полезности блага В поделить на цену В и так далее. Эту формулу ещё называют формулой эффективности Парето.

В реальной жизни потребительского равновесия и эффективности по Парето достигнуть невозможно, потому что полезности благ постоянно меняются в зависимости от изменения обстоятельств и потому что большинство благ нельзя дробить на небольшие части, без чего равенство невозможно.

На практике потребитель находится в состоянии неравновесия. Поэтому, исходя из правила максимизации потребности, мы можем сформулировать Закон потребительского выбора – из всего богатства выбора покупатель приобретёт в первую очередь тот товар, предельная полезность которого на единицу вложенных средств наибольшая.

После покупки данного товара его предельная полезность уменьшается, согласно закону уменьшения предельной полезности. В результате становится более выгодно купить другой товар. Если бы этот процесс продолжался бы при прочих равных условиях, и то в итоге потребитель пришёл бы к состоянию, близкому к состоянию эффективности Парето, только с учётом недробности благ. Но дело в том, что условие «при прочих равных условиях» выполнить невозможно, так как процесс покупки требует времени, а со временем меняется и полезность и (медленнее) цены. Поэтому потребитель всегда стремится к равновесию, но находится в состоянии неравновесия.

Эффект дохода и замещения.