Розподіл Стьюдента
Означення 23.3.Закон розподілу випадкової величини 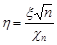 , де величина
, де величина 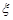 має нормальний розподіл
має нормальний розподіл 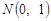 , величина
, величина 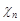 має розподіл “хі з
має розподіл “хі з 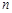 ступенями вільності” та обидві вони незалежні називається розподілом Стьюдентаз
ступенями вільності” та обидві вони незалежні називається розподілом Стьюдентаз 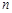 ступенями вільності” (або
ступенями вільності” (або 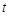 -розподілом).
-розподілом).
Для знаходження щільності розподілу Стьюдента використаємо формулу (21.2) та умову незалежності випадкових величин:
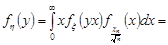
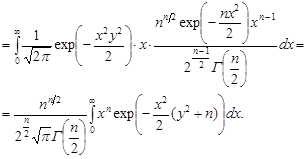
Зробимо заміну змінних
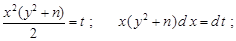
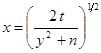 .
.
Тоді щільність розподілу закону Стьюдента набуває вигляду
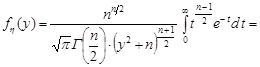
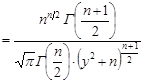 при
при  .
.
При 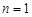 розподіл Стьюдента стає розподілом Коші
розподіл Стьюдента стає розподілом Коші
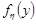
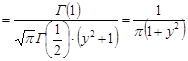 .
.
Оскільки щільність розподілу Стьюдента є парна функція, то всі його початкові моменти непарного порядку дорівнюють нулю, отже,  . Знайдемо значення для моментів парного порядку.
. Знайдемо значення для моментів парного порядку.
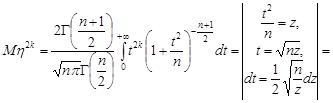
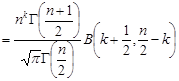 ,
,
де 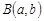 – бета-функція, яка визначається так:
– бета-функція, яка визначається так: 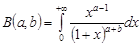 ,
, 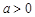 ,
, 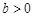 . Як відомо, бета-функція зв’язана з гамма-функцією співвідношенням
. Як відомо, бета-функція зв’язана з гамма-функцією співвідношенням 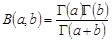 , отже, парні моменти можна записати так:
, отже, парні моменти можна записати так:
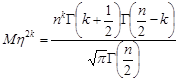 .
.
Покладемо в цій формулі 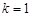 , отримаємо
, отримаємо
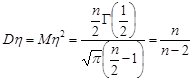 .
.
При 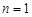 розподіл Стьюдента стає розподілом Коші. А при достатньо великих
розподіл Стьюдента стає розподілом Коші. А при достатньо великих 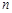
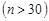 , розподіл Стьюдента набуває значень близьких до нормального розподілу
, розподіл Стьюдента набуває значень близьких до нормального розподілу 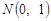 .
.
Дата добавления: 2015-08-14; просмотров: 2070;
