Гамма-розподіл
ЛЕКЦІЯ 23
ДЕЯКІ РОЗПОДІЛИ, ЯКІ ЗАСТОСОВУЮТЬ В МАТЕМАТИЧНІЙ СТАТИСТИЦІ
Питання, що розглядаються в лекції
1. Гамма-розподіл.
2. Розподіл 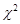 з
з 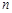 ступенями вільності (розподіл Пірсона).
ступенями вільності (розподіл Пірсона).
3. Розподіл Стьюдента.
4. Розподіл Фішера-Снедекора.
В цій лекції розглядається декілька законів розподілу, які складають необхідний апарат для побудови статистичних критеріїв та оцінок, що застосовуються, перш за все, в математичній статистиці.
Гамма-розподіл
Означення 23.1. Невід’ємна випадкова величина 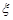 має гамма-розподіл з параметрами
має гамма-розподіл з параметрами 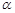 та
та 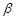 , якщо її щільність розподілу дорівнює
, якщо її щільність розподілу дорівнює
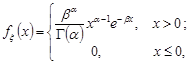
де 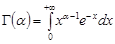 – гамма-функція.
– гамма-функція.
Окремим випадком гамма-розподілу є показниковий розподіл, для якого 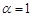 ,
,  . Дійсно, при таких параметрах
. Дійсно, при таких параметрах
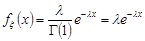 ,
, 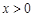 .
.
Знайдемо початкові моменти гамма-розподілу.

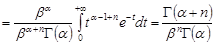 .
.
При 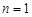 маємо математичне сподівання випадкової величини
маємо математичне сподівання випадкової величини 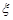
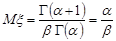 .
.
Другий початковий момент буде таким:
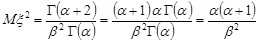 .
.
Отже, дисперсія гамма-розподілу дорівнює
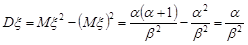 .
.
Приклад 23.1. Скласти композицію двох випадкових величин 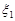 та
та 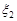 , розподілені за гамма-розподілом із параметрами
, розподілені за гамма-розподілом із параметрами 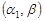 та
та 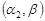 .
.
Розв’язання. За формулою (21.3)
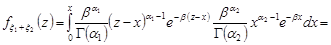
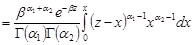 .
.
В останньому інтегралі зробимо заміну 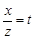 , тоді
, тоді
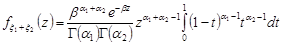 .
.
Оскільки
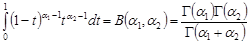 , то при
, то при 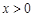
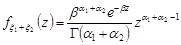 ,
,
тобто також гамма-розподіл з параметрами 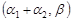 .
.
Дата добавления: 2015-08-14; просмотров: 1588;
