Розподіли та з ступенями вільності
(розподіл Пірсона)
Розглянемо випадковий вектор 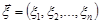 , компоненти якого є незалежними, нормально розподіленими випадковими величинами з параметрами
, компоненти якого є незалежними, нормально розподіленими випадковими величинами з параметрами 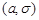 .
.
Означення 23.2. Закон розподілу випадкової величини 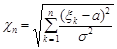 називається розподілом “хі з
називається розподілом “хі з 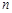 ступенями вільності”.
ступенями вільності”.
Знайдемо функцію та щільність розподілу цієї випадкової величини. Щільність розподілу 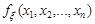 випадкових величин
випадкових величин 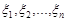 має вигляд
має вигляд
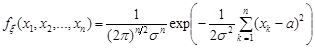 .
.
Функція розподілу випадкової величини 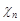 за означенням дорівнює
за означенням дорівнює
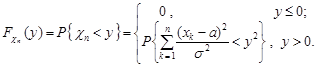
Знайдемо вираз 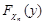 для
для 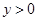 :
:
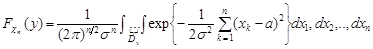 ,
,
де 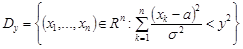 .
.
Введемо заміну 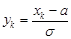 . Тоді
. Тоді
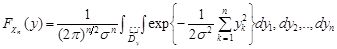 .
.
Застосуємо узагальнені сферичні координати:
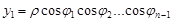 ;
;
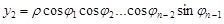 ;
;
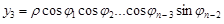
...........
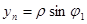 .
.
Тоді 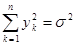 . Якобіан перетворення дорівнює
. Якобіан перетворення дорівнює
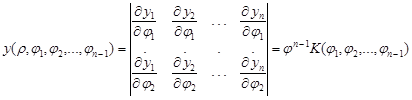 .
.
Область, по якій треба інтегрувати, симетрична відносно початку координат, а підінтегральна функція парна відносно кожної змінної. Отже, достатньо обчислити цей інтеграл тільки по тій частині області, де 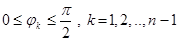 , а результат помножити на відповідне число, яке навіть нема необхідності знати, тобто
, а результат помножити на відповідне число, яке навіть нема необхідності знати, тобто
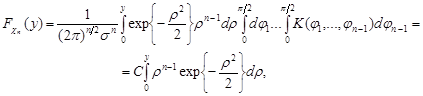 де
де 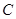 – деяка константа. Обчислимо її, враховуючи, що
– деяка константа. Обчислимо її, враховуючи, що
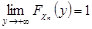 . Маємо
. Маємо 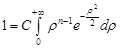 . Отже,
. Отже,
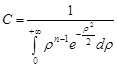 .
.
Введемо заміну змінних 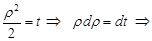
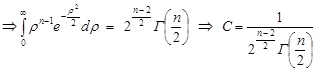 .
.
Остаточно функція розподілу має вигляд
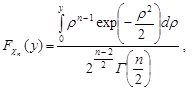 при
при  .
.
Запишемо щільність розподілу випадкової величини 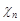 :
:
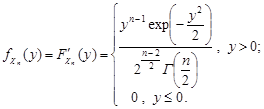
Розглянемо ще одну випадкову величину вигляду 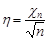 і знайдемо її закон розподілу.
і знайдемо її закон розподілу.
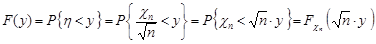 .
.
Отже,
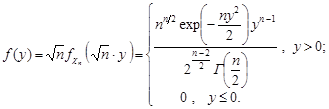
Означення 23.3. Закон розподілу випадкової величини 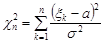 називається розподілом “хі-квадрат з
називається розподілом “хі-квадрат з 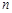 ступенями вільності” ( або розподілом Пірсона).
ступенями вільності” ( або розподілом Пірсона).
Із результатів лекції 20 випливає, що щільності розподілів 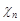 та
та 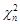 пов’язані співвідношенням
пов’язані співвідношенням 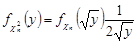 ,
,  .
.
Таким чином,
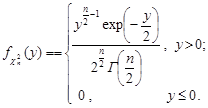
Із вигляду щільності розподілу 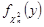 видно, що розподіл
видно, що розподіл 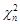 є окремим випадком гамма-розподілу з параметрами
є окремим випадком гамма-розподілу з параметрами 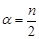 та
та 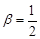 . Отже, числові характеристики розподілу
. Отже, числові характеристики розподілу 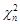 знайдемо з числових характеристик гамма-розподілу:
знайдемо з числових характеристик гамма-розподілу:
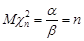 ,
, 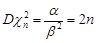 .
.
Дата добавления: 2015-08-14; просмотров: 645;
