Квантові аспекти розподілів. Розподіли Бозе–Айнштайна і Фермі–Дірака
Системи багатьох частинок, для яких застосовні розподіли Максвелла і Больцмана, складаються з частинок, які можна розрізняти за певними ознаками. Якщо ж система складається з однакових нерозрізнюваних частинок, то і їхні статистичні розподіли будуть іншими. З погляду квантової механіки стан мікрочастинки визначений певним набором квантових чисел. Кожному набору квантових чисел відповідає цілком певне значення енергії. Отже, розподіл таких частинок за енергіями зумовлений їхнім розподілом за квантовими станами. Є два квантові статистичні розподіли – Бозе–Айнштайна і Фермі–Дірака. Ці розподіли описують стан систем мікрочастинок, кожна з яких має нульовий або цілий спін, чи напівцілий. Частинки, що мають цілий спін ферміони (це електрони, протони, нейтрони та ін.), а ті, що мають нульовий, – бозонами (це фотони, фонони, мезони та ін.). Різниця між бозе- і фермі-газом полягає в тому, що кількість бозе-частинок з однаковою енергією може бути довільною, тоді як у фермі-газі однакову енергію можуть мати не більше двох частинок з протилежними спінами.
Середню кількість частинок з енергією у проміжку від Е до Е+dE обчислюють за відповідними функціями розподілу:
 – функція розподілу Бозе–Айнштайна, (2.35)
– функція розподілу Бозе–Айнштайна, (2.35)
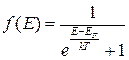 – функція розподілу Фермі–Дірака. (2.36)
– функція розподілу Фермі–Дірака. (2.36)
Зазначимо, що квантові розподіли безпосередньо пов’язані з класичним розподілом Максвелла–Больцмана. Справді, за умови Е>>kТ експонен-ціальний доданок у (2.35) і (2.36) стає суттєво більшим від одиниці, якою можна знехтувати. За цих умов обидва квантові розподіли перетворюються у класичний розподіл Максвелла–Больцмана (2.34).
Дата добавления: 2015-07-22; просмотров: 1074;
