Розподіл Максвелла–Больцмана
У потенціальному полі координати і швидкості молекул газу незалежні, отже, незалежними є й обидва розподіли – Максвелла та Больцмана. Водночас їх можна об’єднати в один розподіл Максвелла–Больцмана, відповідно до якого кількість молекул, компоненти швидкості яких містяться у проміжках vx, vx+dvx; vy, vy+dvy; vz, vz+dvz, а координати, відповідно, – у проміжках x, x+dx; y, y+dy; z, z+dz,
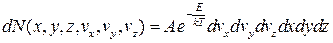 , (2.32)
, (2.32)
де 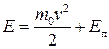 – повна енергія частинки;
– повна енергія частинки; 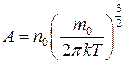 .
.
Якщо у (2.32) зробити перетворення і перейти до змінних Ек і Еп, то
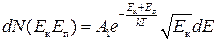 . (2.33)
. (2.33)
Тут
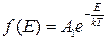 (2.34)
(2.34)
– це функція розподілу Максвелла–Больцмана.
Дата добавления: 2015-07-22; просмотров: 1733;
