Цилиндрическая стенка.
Очень часто теплоносители движутся по трубам и требуется рассчитать тепловой поток, передаваемый через цилиндрическую стенку трубы. Задача о распространении теплоты в цилиндрической стенке при известных и постоянных температурах на внутренней и наружной поверхностях, также одномерная, если ее рассматривать в цилиндрических координатах. Температура изменяется только вдоль радиуса (по координате r), а по длине трубы и по ее периметру остается неизменной. В этом случае dt/drи закон Фурье будет иметь вид
q = -λ (dt/dr) [92]
или для трубы длиной l
Q =Fq =-2πr/λ dt/dr [93]
Интегрировать удобно уравнение[93], так как тепловой поток не меняется по толщине стенки, а q = Q/F ≠ const, поскольку площадь F = 2πrl, через которую проходит тепловой поток, зависит от радиуса.
Разделим переменные: 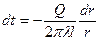 [94]
[94]
Интеграл этого уравнения [94] 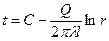 [95]
[95]
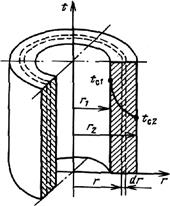
|
| Рис. 2.6 Изменение температуры по толщине однослойной цилиндрической стенки |
У внутренней поверхности, где кривизна стенки больше, температура меняется резче, чем у наружной.
Интегрирование уравнения [94]в определенных пределах (по tот tc1до tc2и по r от r1до г2) дает зависимость для расчета теплового потока через цилиндрическую стенку:
Q = 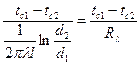 [96]
[96]
Для труб обычно измеряется и приводится в условиях задач диаметр, а не радиус, поэтому отношение радиусов r2/r1 заменено отношением диаметров
d2/d1 Термическое сопротивление для цилиндрической стенки имеет вид
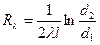 [97]
[97]
причем при d2/d1≈ 1 расчет должен проводиться с высокой точностью, поскольку небольшая погрешность, допущенная при определении отношения d2/d1, в этом случае дает значительную ошибку при вычислении логарифма.
Для определения теплового потока через многослойную цилиндрическую стенку следует, как и для многослойной плоской стенки, просуммировать термические сопротивления отдельных слоев:
Q = 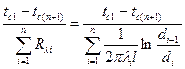 [98]
[98]
Отличие формулы [98]от [90] заключается только в способе расчета термических сопротивлений отдельных слоев для плоской и цилиндрической стенок. Но и это различие существенно только при больших отношениях наружного и внутреннего диаметров каждого слоя dн/dвн = di+1/di > 1,5. При меньших отношениях dн/dвн термические сопротивления отдельных слоев, как уже было показано, целесообразнее считать по упрощенной формуле 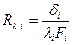 справедливой для плоской стенки.
справедливой для плоской стенки.
Расчет температур на границах слоев в данном случае осуществляется так же, как для многослойной плоской стенки, т. е. по формуле [91] 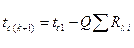
Шаровая стенка. При постоянных температурах tc1 tc2 на внутренней (радиусом r1) и наружной (радиусом r2)поверхностях шаровой стенки температурное поле одномерно в сферических координатах, т. е. температура изменяется только по радиусу. Следовательно, Q = qF = - λF(dt/dr) = -λ4πr2(dt/dr) [99]
Разделив переменные и проинтегрировав по ( в пределах от tc1 и tc2 по rв пределах от r1 до r2: 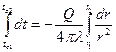 [100]
[100]
получим расчетную формулу для теплового потока через шаровую стенку:
Q = 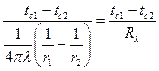 [101]
[101]
Дата добавления: 2015-08-14; просмотров: 1090;
