Распределение компонент непрерывной случайной величины (х ; у).
 |
Закон совместного распределения величин х и у полностью определяет законы распределения каждой из величин х и у. Пусть F(x;y) – плотность совместного распределения величин х и у. Найдем плотность распределения величины х. Рассмотрим вероятность попадания значения величины х в любой интервал от х1 до х2.
т.к. попадание абсциссы в интервале равносильно попаданию точки в вертикальную область D, то вероятности этих событий равны.
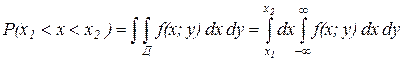
Данный интеграл можно записать и таким образом
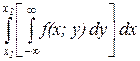
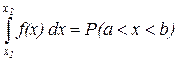
Сравним с другим равенством. Согласно определению плотности распределения следует, что искомая плотность равна
,
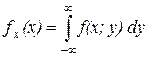Аналогично площадь распределения величины у будет равна
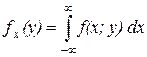
Эти понятия обобщаются для систем более 2-х величин.
Определение: Непрерывные случайные величины х и у называются независимыми, если плотность совместного распределения равна произведению плотности этих величин
-условие независимости.
Дата добавления: 2015-08-14; просмотров: 531;