Функция от случайных величин
Определение: Под функцией j(х) случайной величины Х понимают такую случайную величину у, которая принимает значения у=j(х) каждый раз , когда величина Х принимает значение х.
1. Пусть аргумент Х – дискретная случайная величина с возможными значениями х1, х2, х3, …..хn и вероятностями Р1, Р2, Р3…..Рn . Пусть для различных возможных значений xi, значения функции j(хi) также различны. Возможными значениями случайной величины случайной величины у будут значения функции j(хi) тогда и только тогда, когда величина Х примет значение хi, поэтому вероятности их равны, т.е.
Р(Y=j(хi))=P(X=xi)=Pi
Т.к. событие - величина X приняла значение xi влечет за собой событие-величина у приняла значение уi=j(хi) и обратно эти события равносильны и следовательно равновероятностные.
Пример 1.
Случайная величина задана распределением
| x | -2 | |||
| Р | 0,1 | 0,5 | 0,3 | 0,1 |
Найти закон распределения вероятностей величин х2, 3х, х2+1.
у=х2
| x2 | ||||
| Р | 0,1 | 0,5 | 0,3 | 0,1 |
у=3х
| 3x | -6 | |||
| Р | 0,1 | 0,5 | 0,3 | 0,1 |
у=х2+1
| x2+1 | ||||
| Р | 0,1 | 0,5 | 0,3 | 0,1 |
Пример 2.
Дано распределение
| x | -2 | ||
| Р | 0,4 | 0,5 | 0,1 |
Найти распределение величины у=х2
| x | |||
| Р | 0,4 | 0,5 | 0,1 |
Событие х2=4 есть сумма 2-х событий х=-2 и х=2, поэтому по правилу сложения вероятностей
Р(х2=4)=0,4+0,5=0,9
Тогда пишут
| У | ||
| Р | 0,9 | 0,1 |
Пример 3. даны две независимые случайные величины х и у.
| Х | -1 | ||
| Р | 0,2 | 0,3 | 0,5 |
| У | |||
| Р | 0,1 | 0,3 | 0,6 |
Составить закон распределения величины z=(х×у)
| N | x | y | x×y | P |
| -1 -1 -1 | 0,02 0,06 0,12 0,03 0,09 0,18 0,05 0,15 0,3 | -1 -3 |
Р(z=0)=0,03+0,09+0,18+0,05+0,02+0,02+0,08+0,27=0,37
| z | -3 | -1 | |||
| Р | 0,12 | 0,06 | 0,37 | 0,15 | 0,3 |
Т.к. случай z=0 – несовместимое событие, то по теореме сложения Р(0) складываем.
2) Пусть аргумент x непрерывная случайная величина. Как найти распределение функции у=j(х), зная плотность распределения f(x) аргумента x.
Рассмотрим монотонную функцию от одной случайной величины. Пусть в интервале возможных случайных значений х (a;b) функция строго возрастает, т.е. если х2>х1 то у2>у1 .
Пусть аргумент x непрерывная случайная величина. Как найти распределение y=j(x), зная плотность распределения f(x) случайного аргумента x. Рассмотрим монотонную функцию от одной случайной величены. Пусть в интервале возможных значений от а до b функция строго возрастает.
 |
Кроме того , функция непрерывна вместе со своей 1-ой производной и имеет непрерывную дифференцируемую функцию, каждый внутренний интервал от x1 до х2 взаимно однозначно отображается на соответствующем интервале от у1 до у2 потому: Р(у1<у<у2)=Р(х1<x<x2) вероятности попадания случайной величены х и у это есть двумерная величена.
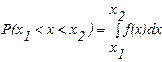 -двумерная величина.
-двумерная величина.
В этом интервале заменяем х на функцию g(y) обратную к функции y=j(x)
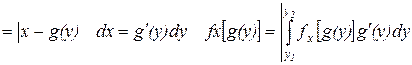
сравнивая с равенством (1) мы отмечаем, что подинтегральная функция – есть плотность распределения непрерывности случайной величены у.
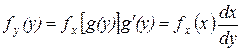 в дифференцируемой форме
в дифференцируемой форме 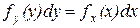 .
.
Дата добавления: 2015-08-14; просмотров: 761;
