Модели представления знаний.

В ИИ-области традиционновыделяются две группы методов представлений знаний – декларативные и процедурные [58-60].

6.2.1. Декларативные методы: логические и сетевые модели.

В декларативных методах знания – это структурированные данные, для представления которых используются логические или сетевые модели.

В логической модели знания представляются в виде формальной системы С_l, задаваемой тройкой (П;Р;В), где П={П₁;…;П_k} – набор системных множеств, определяющих предметную область представляемых знаний; Р={Р₁; …;Р_m} – наборотношений между системными множествами, определяющих грамматику, в рамках которой из элементов системных множеств образуются синтаксически правильные выражения; В={В₁;…;В_n} – совокупность правил логического вывода в рамках данной предметной области и грамматики. Кроме того, для компонентов наборов П;Р;В устанавливаются процедуры, реализующие идентификацию их элементов и, соответственно, их принадлежность.

В сетевых моделях знания представляются в виде орграфа C_s, определяемого тройкой (V;E;I), где V={V₁;…:V_k} – набор классов объектов (сущностей), элементы которых определяют вершины предметной области представляемых знаний; E={E₁;…;E_m} – набор типов ориентированных ребер (дуг), определяющих типы связей (отношений) между вершинами рассматриваемой предметной области знаний; I – набор отношений инцидентности между вершинами и дугами на орграфе С_s. Особенность орграфа С_s состоит в том, что он представляет собой сеть, т.е. в нем всегда выделяется набор вершин – источников, из которых дуги только выходят, и, довольно часто, источники сети С_s связаны с аксиоматикой рассматриваемой области знаний. Что касается вершин-стоков, то их всегда можно выделить, если сеть С_s – конечная, как это имеет место, например, при изучении некоторой предметной дисциплины в учебном процессе. Если же сеть С_s конечной не является, как это имеет место, например, при построении аксиоматической теории [10], то в этом случае стоки «достигаются» только лишь виртуально, в процессе некоторой потенциально бесконечной процедуры развития этой теории.

В зависимости от типа связей, используемых для представления знаний, различают классифицирующие сети, функциональные сети и сценарии [60]. В классифицирующих сетях используются отношения структуризации (т.е. частичного порядка), позволяющие вводить те или иные иерархические отношения между информационными единицами данной области знаний. Функциональные сети характеризуются наличием функциональных отношений, с помощью которых реализуют соответствующие процедуры необходимых «вычислений», выражая одни информационные единицы знаний через другие. В сценариях используются так называемые каузальные (причинные) отношения или отношения вроде «средство-результат», «орудие-действие» и т.п.

Отметим, что, если в сетевой модели имеют место связи различного типа, то такую модель обычно называют семантической сетью. Важно подчеркнуть, что между логической и сетевой моделями представления знаний принципиальной разницы нет и, вообще говоря, между ними довольно легко устанавливается изоморфизм С_l 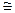C_s. Поэтому выбор той или иной модели (С_l или C_s) в каждом случае, главным образом, определяется удобством ее конкретной реализации.

6.2.2. Процедурные методы: продукционные модели и фреймы.

В процедурных методах знания также представляются структуриро-ванными данными, но при этом с элементами структур могут быть связаны определенные специализированные процедуры и в современных ИИ-системах эти методы реализуются, в основном, в виде продукционных и фреймовых моделей [60].

Продукционные модели представляют собой некоторую комбинацию из элементов логических и сетевых моделей: из логических моделей берется идея правил вывода, которые здесь называются продукциями, а из сетевых моделей – описание знаний в виде семантической сети. Применение правил логического вывода к фрагментам сетевого описания знаний приводит к преобразованию семантической сети (исключение ненужных фрагментов, наращивание сети и т.п.) и, таким образом, в продукционных моделях процедурная информация явно выделена и описывается иными формальными средствами, чем декларативная информация. В результате в продукционных моделях, в отличие от логических, появляется вывод на знаниях. Что касается фреймовых моделей, то, по сути, они объединили в себе все основные идеи рассмотренных моделей представления знаний и, в связи с этим, имеется точка зрения, по которой нет особой необходимости специально выделять фреймовые модели в представлении знаний [60]. Действительно, фреймовая модель предполагает структуризацию фреймов по «принципу матрешки», что требует задания процедурной информации, обеспечивающей переход от одного фрейма к другому, и при этом устройство каждого фрейма реализуется посредством декларативной информации в рамках логической или сетевой модели, т.е. фреймовая модель в одном лице сочетает логическую, сетевую и продукционную модели.

Разумеется, в теории представления знаний можно рассматривать вопросы оптимизации, т.е. выяснять, в каких случаях та или иная модель представления знаний оказывается более эффективной. Однако специфика оптимизации в этом случае сильно зависит от операций, которые в дальнейшем будут проводиться на основе представленных знаний.

Библиография к части 1.

1. Кибернетика // Математическая энциклопедия. В 5 т.: Т. 2. – М.: Советская Энциклопедия, 1976. – С. 850.

2. Платон. Диалоги. – М.: Мысль, 1986. – 607 с.

3. Поваров Г.Н. Ампер и кибернетика. – М.: Советское радио, 1977. – 96 с.

4. Богданов А.А. Тектология. Всеобщая организационная наука. В 2-х кн. – М.: Экономика, 1989.- Кн.1- 303 с. Кн.2- 350 с.

5. Шеннон К. Работы по теории информации и кибернетике.– М.: ИЛ, 1963. 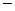829 с.

6. Винер Н. Кибернетика или управление и связь в животном и машине. – М.: Советское радио, 1968. – 326 с.

7. Глушков В.М. Кибернетика. Вопросы теории и практики.– М.: Наука, 1986. – 488 с.

8. Стариченко Б.Е. Теоретические основы информатики. – М.: Горячая линия – Телеком, 2003. – 312 с.

9. Яглом А.М., Яглом И.М. Вероятность и информация. – М.: Наука, 1973. – 511 с.

10. Фирстов В.Е. Кибернетическая концепция и математические модели управления дидактическими процессами при обучении математике в школе и вузе // Монография. – Саратов: Издательский Центр «Наука», 2010. – 511 с.

11. Арнольд В.И. «Жесткие» и «мягкие» математические модели. – М.:Изд-во Московского центра непр. обр., 2004. – 32 с.

12. Бонгард М.М. Проблема узнавания. – М.: Наука, 1967. – 320 с.

13. Вапник В.Н., Червоненкис А.Я. Теория распознавания образов.– М.: Наука, 1974. – 415 с.

14. Лидл Р., Пильц Г. Прикладная абстрактная алгебра // Под ред. Л.Н. Шеврина. – Екатеринбург: Изд-во Урал. ун-та, 1996. – 744 с.

15. Пегат А. Нечеткое моделирование и управление. – М.: БИНОМ, Лаборатория знаний, 2009. – 798 с.

16. Колмогоров А.Н. Три подхода к определению понятия «количество информации» // Проблемы передачи информации, 1965, т.1, №1. – С. 3-11.

17. Урсул А,Д, Природа информации. - М.: Политиздат, 1968. – 288 с.

18. Ительсон Л.Б. Математические и кибернетические методы в педагогике. – М.: Просвещение, 1964. – 248 с.

19. Моль А. Теория информации и эстетическое восприятие. – М.: Мир, 1966. – 352 с.

20. Rashevsky N. Live, Information Theory and Topology // The Bulletin of Mathematical Biophysics. – Chicago, 1955, V.17, №3. – P. 25-78.

21. Вагин В.Н., Викторова Н.П. Вопросы структурного обобщения и классификации в системах принятия решений // Изв. АН СССР. Техническая кибернетика, 1982, №5. – С. 64-72.

22. Хакен Г. Информация и самоорганизация. – М.:Ком. Книга, 2005.–248 с.

23. Пер Бак, Кан Чен. Самоорганизованная критичность // В мире науки, 1991, №3. – С. 16-24.

24. Аристотель. О душе. Соч. в 4-х т. Т.1. – М.: Мысль, 1975. – С. 369-448.

25. Кант И. Критика чистого разума. – М.: Мысль, 1994. – 591 с.

26. Холодная М.А. Психология интеллекта. – СПб.: Питер, 2002. – 272 с.

27. Блонский П.П. Предисловие к сборнику «Тесты: теория и практика». №1. – М.: Работник просвещения, 1928. – 80 с.

28. Glaser R.Education and thinking: The role of knowledge // Amer.Psychologist., 1984,V.39, №2. – P. 93-104.

29. Аристотель. Сочинения в 4-х т. Т.2. – М.: Мысль, 1978. – 687 с.

30. Игошин В.И. Математическая логика и теория алгоритмов. – М.: Издательский центр «Академия», 2004. – 448 с.

31. Минский М. Искусственный разум // Сб. Информация. – М.: Мир, 1968. –222 с.

32. Малинецкий Г.Г. Математические основы синергетики: Хаос, структуры, вычислительный эксперимент.– М.: Издательство ЛКИ, 2007. – 312 с.

33. Пенроуз Р. Новый ум короля: О компьютерах, мышлении и законах физики. – М.: Едиториал УРСС, 2005. – 400 с.

34. Цыпкин Я.З. Основы теории обучающихся систем. – М.: Наука, 1970. – 252 с.

35. Приобретение знаний. / Под ред. С. Осуги, Ю. Саэки – М.: Мир, 1990. – 304 с.

36. Anderson R. John. The architecture of cognition. – Cambridge (Massachusetts, USA): Harvard Univ. Press, 1983. – 163 p.

37. Кроль В.М. Психология и педагогика. – М.: Высшая школа, 2004. – 325 с.

38. Минский М. Структура для представления знания // Психология машинного зрения. – М.: Мир, 1978.– С. 249-320.

39. Декарт Ренэ. Рассуждение о методе.–М.-Л.:Изд-во АН СССР,1953.– 656 с.

40. Пуанкаре Анри. О науке.–М.:Наука,1983.–560 с.

41. Пушкин В.Н. Психология и кибернетика. – М.: Педагогика, 1971. – 232 с.

42. Меморандум американских математиков // Математика в школе, 1964, №4. – С. 90-92.

43. Адамар Ж. Исследование психологии процесса изобретения в области математики. – М.: Советское радио, 1970. – 152 с.

44. Биркгофф Г.Математика и психология.– М.: Советское радио, 1977.– 96 с.

45. Зиман Э., Бьюнеман О. Толерантные пространства и мозг // В кн. На пути к теоретической биологии. – М.: Мир, 1970. – С. 134-144.

46. Бруннер Дж. Процесс обучения.–М.:Изд-во АПН РСФСР, 1962.– С. 53-64.

47. Столяр А.А. Логическое введение в математику.– Минск: Вышэйшая школа, 1971. – 222 с.

48. Столл Р.Р. Множества. Логика. Аксиоматические теории.– М.: Просвещение, 1968. – 232 с.

49. Барвайс Дж. Введение в логику первого порядка // Справочная книга по математической логике. Часть I: Теория моделей. – М.: Наука, 1982. – С. 13-54.

50. Поспелов Д.А. Логико-лингвистические модели в системах управления.– М.: Энергоиздат, 1981. - 231 с.

51. Редько В.Г. Эволюционная биокибернетика // Сер.: «Кибернетика: неограниченные возможности и возможные ограничения». – М.: Наука, 2001. – 156 с.

52. Чолаков В. Нобелевские премии. Ученые и открытия. – М.: Мир, 1987. – 368 с.

53. Эрдниев П.М.,Эрдниев Б.П.Укрупнение дидактических единиц в обучении математике. – М.: Просвещение, 1986. – 255 с.

54. Коржуев А.В., Попков В.А., Рыбак Е.В. Симметрия и асимметрия в теории обучения в высшей школе // Педагогика, 2004, № 5. – С. 40-45.

55. Паташинский А.З., Покровский В.Л. Флуктуационная теория фазовых переходов. – М.: Наука, 1982. – 382 с.

56. Сергиевский В. Путь к творческому мышлению // Alma mater (Вестник высшей школы), 1991, №7. – С. 12-16.

57. Евин И.А. Синергетика мозга и синергетика искусства.– М.: Геос, 2001.– 164 с.

58. Осуга С. Обработка знаний. – М.: Мир, 1989. – 293 с.

59. Представление и использование знаний / Под ред. Х. Уэно, М. Исидзука. – М.: Мир, 1989. – 220 с.

60. Искусственный интеллект. Справочник. В 3-х кн. Кн. 2. Модели и методы: / Под ред. Д.А. Поспелова. – М.: Радио и связь, 1990. – 304 с.