Частотно-избирательные цепи при узкополосных входных воздействиях.
Узкополосный сигнал – это когда в пределах полосы пропускания меняется 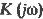 .
.
Пусть входным сигналом служит узкополосное (квазигармоническое колебание) с центральной частотой 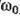 .
.
 (7) спектр входного сигнала и его комплексная огибающая
(7) спектр входного сигнала и его комплексная огибающая
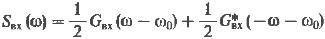 (8)
(8)
Используя спектральный метод и введя замену переменной 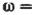
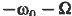 можно после нескольких преобразований получить
можно после нескольких преобразований получить
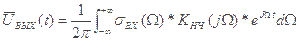 (9) т.е.
(9) т.е.
 (10) спектр плотности огибающей.
(10) спектр плотности огибающей.
Т.е.комплексная огибающая выходного сигнала представляет собой медленно меняющее во времени колебание со спектральной плотностью.
Чтобы решить задачу о прохождении узкополосного сигнала через частотно-избирательную систему следует вначале найти результат воздействия входной комплексной огибающей на НЧ эквивалент исходной системы, а затем перейти к физическому выходному сигналу.
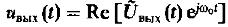 (11)
(11)
Равенство (9) соответствует спектральному методу нахождения сигнала на выходе системы в равной мере могут быть использованы и другие известные методы – операторный метод, интеграл. Дюамеля и т.д.
Например по интегралу Дюамеля
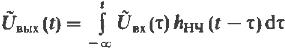 (12) где
(12) где 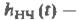 импульсная характеристика НЧ эквивалента.
импульсная характеристика НЧ эквивалента.
Воздействие АМ – сигнала на одноконтурный резонансный усилитель.
Рассмотрим прохождение АМ – сигнала на одноконтурный резонансный усилитель:
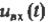
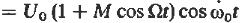 (13)
(13)
Через одноконтурный резонансный усилитель с частотным коэффициентом передачи.
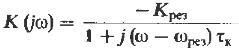 (14) допустим, что
(14) допустим, что 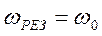 , где
, где 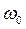 - частота несущее колебание, тогда
- частота несущее колебание, тогда
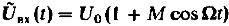 (15)
(15)
Частотный коэффициент передачи НЧ – эквивалентного усилителя.
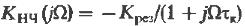 (16)
(16)
Выходную комплексную огибающую найти из 15. Применив обычный метод комплексных амплитуд.
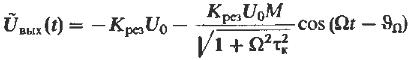 (17) где
(17) где 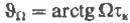 фазовый сдвиг.
фазовый сдвиг. 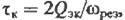 получим:
получим:
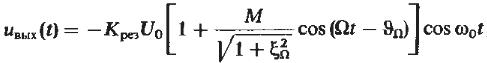 (18)
(18)
Где 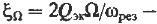 обобщённая расстройка колебательного контура на верхней боковой частоте.
обобщённая расстройка колебательного контура на верхней боковой частоте.
На выходе резонансного усилителя существуют колебание, которое будучи усиленным по амплитуде по прежнему является однотональным АМ – сигналом. Однако коэффициент модуляции на выходе меньше, чем на входе:
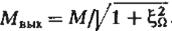 (19)
(19)
Огибающая на выходе запаздывает относительно огибающей входного сигнала на время
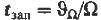 .
.
Дата добавления: 2015-08-14; просмотров: 1187;
