Модель дуополии Курно.

Модели дуополии позволяют проиллюстрировать как предположения отдельного продавца относительно ответа соперника воздействуют на равновесный выпуск.

Статический анализ взаимоотношения двух фирм в условиях дуополии был предложен в 1838 г. Французским экономистом Антуаном Огюстьеном Курно.

Модель дуополии Курно допускает, что каждый из двух продавцов предполагает:что его конкурент будет удерживать свой выпуск неизменным, на текущем уровне, что продавцы не узнают о своих ошибках.

Модель Курно базируется на двух основных предположениях о поведении фирмы в условиях дуополии:

1) каждая фирма нацелена на максимизацию получаемой прибыли;

2) каждая фирма предполагает, что при изменении собственно объёма выпуска другая фирма сохранит свой выпуск на существующем уровне.

В этих условиях достижение равновесия на рынке будет выглядеть следующим образом.

Предположим, что в регионе есть только два продавца («А» и «В») идентичного товара. Вход на рынок этого товара невозможен для других продавцов. Допустим, что оба продавца выпускают этот товар при одинаковых затратах. Допустим, что фирма «А» начинает производить первой, облает всем рынком и предполагает, что на рынке не будет соперников. В этом случае «А» ведет себя как монополия, а поэтому её и объём и цена являются монопольными. Сразу же после того как фирма «А» начинает производство, появляется фирма «В». Появление новы фирм не предвидится. Фирма «В» предполагает, что «А» не будет изменять достигнутый объём производства и объём продаж. Фирма «В» увеличит рыночное предложение, что вызовет уменьшение цены на данный товар. «В» каждый период будет увеличивать выпуск, а «А» каждый месяц снижать свой выпуск. Конечный равновесный выпуск каждой фирмы достигает 1/3 конкурентного выпуска. Общий рыночный выпуск равен 2/3 равновесного конкурентного выпуска при данном спросе на товар. Следовательно, процесс достижения равновесия на рынке выглядит следующим образом: одно из предприятий выбирает объём выпуска продукции, максимизирующий его собственную прибыль, затем второе предприятие, предполагая, что уровень выпуска продукции остаётся неизменным, определяет собственную максимизирующую прибыль и объём продаж. Это равновесие Курно для дуополии.

Равновесие Курно –это некооперативное равновесие: каждая фирма принимает решения, которые дают наибольшие возможные прибыли при данных действиях своих конкурентов.

Равновесие в модели Курно можно представить через кривые реагирования, которые показывают максимизирующие размеры выпуска, которые будут осуществляться одной фирмой, если даны размеры выпуска другой фирмы-соперника.

Ф.М. Шерер и Д. Росс дают количественную интерпритацию модели Курно. Условиями этой ситуации является то, что вход в отрасль заблокирован. На рынке действуют две фирмы, продукты каждой фирмы идентичны. Каждая фирма обладает одними и теми же постоянными предельными издержками производства. Отраслевой спрос имеет линейную динамику.

Каждая фирма имеет свой уровень производства (q_А и q_В соответственно). Рыночная цена является линейной функцией отраслевого объёма производства:

P(Q) = a – в ,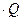

где Q= q_А + q_В.

Прибыль фирмы «А» - это разница между общим доходом 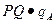и общими издержками, которые равны произведению постоянных средних издержек (С) на объём производства продукции:

.

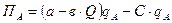Модель Курно основана на предпосылке, что каждая фирма исходит из постоянного объёма выпуска другой фирмы. При этой предпосылке фирма «А» максимизирует свою прибыль, дифференцируя П_А по q_А и приравнивая полученное выражение к нулю (условие существования максимума функции прибыли первого порядка):

.

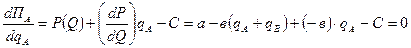Преобразовав уравнение получаем:

.

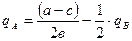Данное уравнение связывает уровень производства фирмы «А» с объёмом производства фирмы «В». Это уравнение является функцией реакции, или кривой реакции, поскольку оно регистрирует максимизирующую прибыль ответа «А» на решения фирмы «В».

Фирма «В» имеет свою функцию реакции, или кривой реакции, которая основана на учёте действий фирмы «А».

.

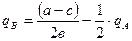Равновесное решение обеих фирм лежит на пересечении двух кривых реакций и означает решение проблемы максимизации прибыли, свидетельствующее о том, что дальнейшее изменение объёмов выпуска для обеих фирм нецелесообразно.

Значение равновесного объёма производства продукции определяется по формуле:

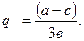
Пример: линейная функция спроса имеет вид: Р(Q)=200 – Q, а=200, в=1

У каждой фирмы постоянные издержки С=50.

Т.о. прибыль фирмы «А» равна: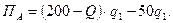

Функция реакции фирмы «А» может быть найдена при принятых значениях а, в, с:

.

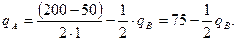Функция реакции фирмы «В»: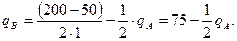

Равновесное решение: .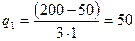

Поскольку фирмы «А» и «В» идентичны, мы можем поставить эти значения в первую формулу и определить отраслевую цену: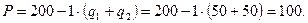

В том случае, когда на рынке представлено «n» фирм с одинаковыми предельными издержками, каждая фирма обладает ограниченной монопольной властью, т.е. цена устанавливается выше предельных издержек; разница между ценой и издержками уменьшается по мере роста числа фирм и эластичности рыночного спроса (Е):

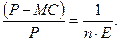
Для фиксированного «n» величина разности уменьшается по мере роста эластичности спроса.

С ростом числа фирм равновесная цена снижается до тех пор, пока она не станет равной предельным издержкам; т.е. по мере роста числа фирм равновесие становится всё более конкурентным.

Если предельные издержки (МС) различаются от фирмы к фирме, доля каждой фирмы (S_i) зависит от её эффективности. Фирма с более низкими издержками будет обладать большей рыночной долей: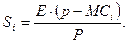

Наконец, модель Курно устанавливает прямую связь между функционированием отрасли, измеряемым различием между ценой и взвешенными средними отраслевыми предельными издержками (МС), а также уровнем рыночной концентрации, измеренным по индексу Герфиндаля-Хиршмана:

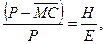
где Н – индекс Герфиндаля-Хиршмана.

Следовательно, основная модель Курно предсказывает тенденцию снижения цены до уровня предельных издержек по мере роста числа продавцов (т.е. в отрасли с меньшим уровнем концентрации цены, вероятнее всего, будут ближе к уровню, который установился бы в результате конкуренции).