Оператор Гамильтона и векторные дифференциальные операции второго порядка.
Оператор Гамильтона (Оператор набла) - это векторный дифференциальный оператор, который в декартовых координатах определяется формулой:
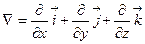
Сам вектор  не имеет реального значения, он приобретает определённый смысл лишь в комбинации со скалярными или векторными функциями.
не имеет реального значения, он приобретает определённый смысл лишь в комбинации со скалярными или векторными функциями.
Представим grad, div и rot через оператор набла:
1. Произведение вектора  на скалярную функцию
на скалярную функцию 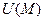 даёт градиент этой функции
даёт градиент этой функции
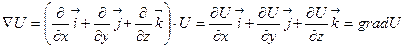 .
.
2. Скалярное произведение вектора  на векторную функцию
на векторную функцию 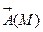 даёт дивергенцию этой функции
даёт дивергенцию этой функции
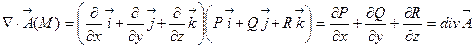 .
.
3. Векторное произведение вектора  на векторную функцию
на векторную функцию 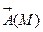 даёт ротор этой функции
даёт ротор этой функции
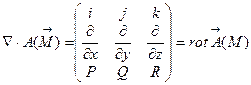 .
.
Действия взятия градиента, дивергенции, ротора называются векторными дифференциальными операциями первого порядка, т.к. в них участвуют только первые производные.
В приложениях встречаются векторные дифференциальные операции второго порядка.
Оператор 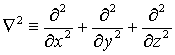 называется оператор Лапласа в декартовых координатах.
называется оператор Лапласа в декартовых координатах.
Дифференциальные операторы второго порядка: 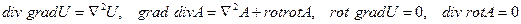
Дата добавления: 2015-08-14; просмотров: 1032;
