Циркуляция

Термин «циркуляция» был первоначально введен в гидродинамике для расчета циркуляции жидкости по замкнутому каналу. Рассмотрим течение идеальной несжимаемой жидкости. Выберем произвольный контур Γ. Мысленно представим, что мы заморозили всю жидкость в объеме, за исключением тонкого канала, включающего в себя контур Γ. Тогда, в зависимости от первоначального характера течения жидкости, она будет либо неподвижной в канале, либо двигаться вдоль контура (циркулировать). В качестве характеристики такого движения берут величину равную произведению скорости движения жидкости по каналу v' на длину контура l. C = v'l

Так как при затвердевании стенок канала нормальная к контуру компонента скорости будет погашена, жидкость по каналу будет двигаться с тангенциальной составляющей исходной скорости v_τ. Тогда циркуляцию можно представить в виде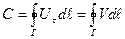

где dl — элемент длины контура.

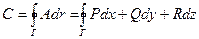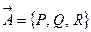Определение. Циркуляцией векторного поля называется криволинейный интеграл второго рода, взятый по произвольному замкнутому контуру Γ. По определению , где — векторное поле (или вектор-функция), определенное в некоторой области D, содержащей в себе контур Γ, 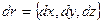— бесконечно малое приращение радиус-вектора 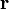. Окружность на символе интеграла подчёркивает тот факт, что интегрирование производится по замкнутому контуру.