Пример. Рассмотрим параметрический синтез комплексной системы измерения высоты, которая использует сигнал от радиовысотомера и баровысотомера.
Рассмотрим параметрический синтез комплексной системы измерения высоты, которая использует сигнал от радиовысотомера и баровысотомера.
Радиовысотомер имеет стационарную флуктуационную ошибку 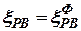 , описываемую корреляционной функцией:
, описываемую корреляционной функцией:
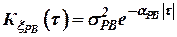 . .
| (13) |
Барометрический высотомер кроме стационарной флуктуационной составляющей ошибки 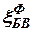 , которая описывается корреляционной функцией
, которая описывается корреляционной функцией
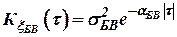 , ,
| (14) |
имеют регуляторную нестационарную составляющую
 , ,
| (15) |
где 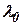 - центрированная случайная величина с заданной дисперсией
- центрированная случайная величина с заданной дисперсией 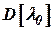 .
.
Таким образов
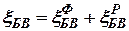 . .
| (16) |
Спектр флуктуационной ошибки радиовысотомера значительно шире спектра аналогичной ошибки баровысотомера ( 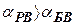 ), поэтому для реализации комплексной системы измерения высоты рационально выбрать схему с фильтром сигнала равной разнице сигналов на низкой частоте, то есть обработку информации измерителей осуществлять согласно схеме компенсации, изображенной на рис. 6.
), поэтому для реализации комплексной системы измерения высоты рационально выбрать схему с фильтром сигнала равной разнице сигналов на низкой частоте, то есть обработку информации измерителей осуществлять согласно схеме компенсации, изображенной на рис. 6.

Рисунок 6
Вид передаточной функции фильтра, с целью выделения регуляторной составляющей ошибки баровысотомера, определяется из условий обеспечения астатизма первого порядка, то есть:
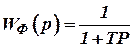 , ,
| (17) |
где постоянная времени 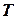 определяется из условий минимизации среднеквадратической ошибки комплексной системы.
определяется из условий минимизации среднеквадратической ошибки комплексной системы.
В данном случае параметрическую минимизацию удобнее проводить в частотной области. Переходя к спектральным характеристикам ошибок, имеет выражение для спектральной плотности РВ:
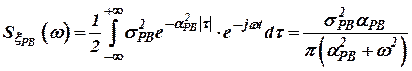 , ,
| (18) |
аналогично спектральная плотность БВ:
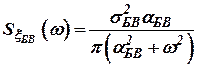 . .
| (19) |
С учетом того, что 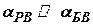 , спектр ошибки радиовысотомера в полосе пропускания фильтра низких частот практически постоянный и равняется значению спектральной плотности при
, спектр ошибки радиовысотомера в полосе пропускания фильтра низких частот практически постоянный и равняется значению спектральной плотности при 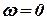 .
.
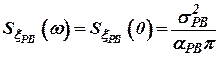 . .
| (20) |
Таким образом, ошибку радиовысотомера можно считать белым шумом.
Составляющие ошибки комплексной системы 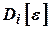 с учетом ошибок отдельных измерителей имеет вид
с учетом ошибок отдельных измерителей имеет вид
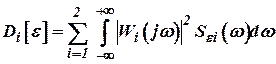 , , 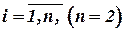 . .
| (21) |
Передаточная функция фильтра для сигнала 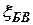 равна
равна 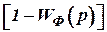 , и в таком случае автоматически выполняются условия инвариантности при будь каких параметрах фильтра
, и в таком случае автоматически выполняются условия инвариантности при будь каких параметрах фильтра 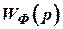 . Соответственно дисперсии ошибок БВ и РВ в соответствии с формулой (21) имеем
. Соответственно дисперсии ошибок БВ и РВ в соответствии с формулой (21) имеем
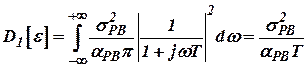 ; ;
| (22) |
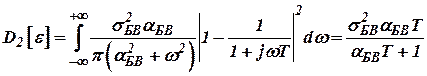 . .
| (23) |
Дисперсия ошибки комплексной системы с учетом независимости ошибок измерителей определяется как
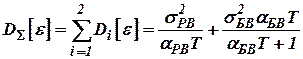 . .
| (24) |
Выражение (24) является целевой функцией, которую необходимо минимизировать относительно параметра 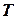 . Ограничением на параметр
. Ограничением на параметр 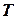 есть только его позитивность.
есть только его позитивность.
Обозначим:
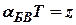 ; ; 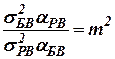 . .
| (25) |
Тогда с учетом (25) выражение (24) представим как:
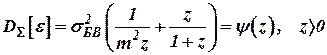 . .
| (26) |
Минимум функции 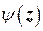 определяется из условия
определяется из условия
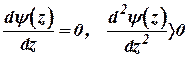 . .
| (27) |
После дифференцирования (26) и приравнивания 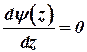 имеем квадратичное уравнение
имеем квадратичное уравнение
 , ,
|
откуда
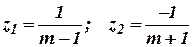 . .
|
Значение 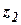 не удовлетворяет условию
не удовлетворяет условию 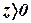 , то есть позитивности
, то есть позитивности 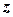 . При
. При 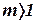 ,
, 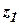 также
также 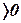 , что выполнятся, так как
, что выполнятся, так как 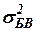 и
и 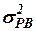 имеют один порядок, а
имеют один порядок, а 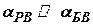 . Таким образом, решением (27) является
. Таким образом, решением (27) является 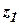 .
.
Исследуя условия для 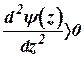 , получим
, получим
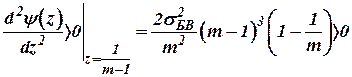 , ,
|
то есть 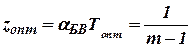 , действительно определяет минимум функции
, действительно определяет минимум функции 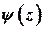 , заданной формулой (26).
, заданной формулой (26).
Оптимальное значение постоянной времени 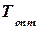 определяется в виде
определяется в виде
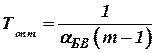 .
.
Дата добавления: 2015-08-14; просмотров: 1116;
