Схема компенсации
Предположим, один и тот же навигационный параметр измеряется двумя или несколькими измерителями, выполненными на различных физических принципах. Тогда алгоритм компенсации, позволяющий снизить погрешность измерения данного навигационного параметра, может быть реализован согласно схеме:
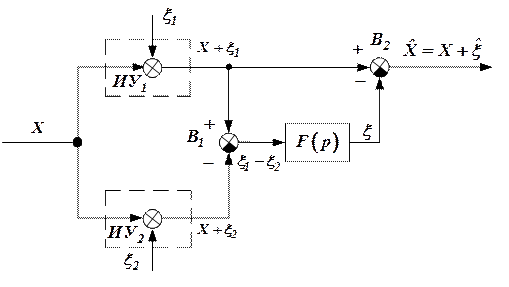
Рисунок 1
Сигналы измерительных устройств 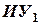 , и
, и  кроме измеряемой величины
кроме измеряемой величины  содержат в себе сигналы ошибок
содержат в себе сигналы ошибок 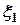 ,
, 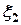 и поступают на вход вычитателя
и поступают на вход вычитателя 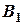 . На входе
. На входе 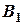 формируется сигнал
формируется сигнал
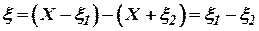 .
.
Сигнал 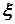 пропускается через динамический фильтр
пропускается через динамический фильтр 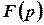 и поступает на вход вычитателя
и поступает на вход вычитателя 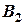 , на выходе которого имеем
, на выходе которого имеем
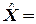
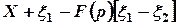
или
 ,
,
где  - ошибка комплексной системы.
- ошибка комплексной системы.
Обычно фильтр низких частот в простейшем случае представляет собой апериодическое звено:
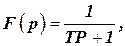
| (1) |
где 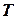 - постоянная времени.
- постоянная времени.
Передаточная функция фильтра высоких частот
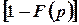 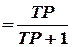
| (2) |
практически представляет собой реальное дифференцирующее звено.
С учетом передаточных функций фильтров (1) и (2) исходная схема (рис.1) для получения 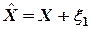 представлена на рис. 2.
представлена на рис. 2.
Учитывая прогнозируемый характер спектральных характеристик 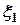 и
и 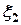 - спектральных плотностей
- спектральных плотностей 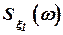 и
и 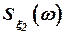 (рис. 3), можно показать графики спектральных характеристик сигналов ошибок
(рис. 3), можно показать графики спектральных характеристик сигналов ошибок 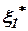 и
и 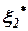 в виде дисперсий ошибок
в виде дисперсий ошибок 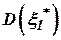 и
и 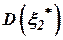 , полученных в результате прохождения сигналов через соответствующие фильтры с амплитудно-частотными характеристиками (АЧХ)
, полученных в результате прохождения сигналов через соответствующие фильтры с амплитудно-частотными характеристиками (АЧХ) 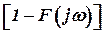 и
и 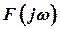 .
.
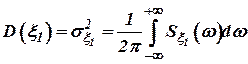 ; ;
| (3) |
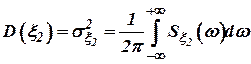 , ,
| (4) |
где 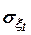 ,
, 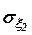 - среднеквадратические ошибки выходных сигналов.
- среднеквадратические ошибки выходных сигналов.
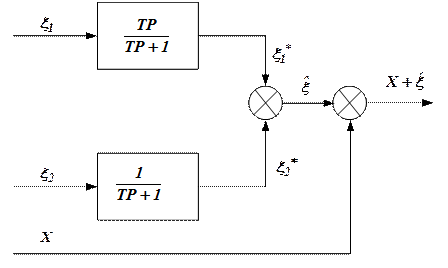
Рисунок 2
Спектральная плотность 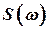 для функции
для функции 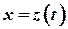 определяется с помощью соотношения Хинчина-Винера.
определяется с помощью соотношения Хинчина-Винера.
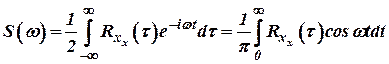 , ,
|
где 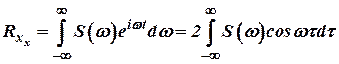 .
.
В свою очередь функция 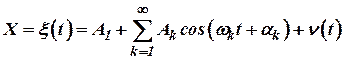 .
.
Если 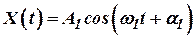 , то
, то  .
.
Дисперсия ошибки системы при реализации способа компенсации имеет вид:
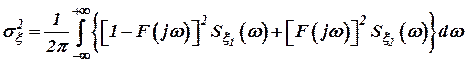 . .
| (5) |
На основании рис. 3 можно сделать вывод о том, что дисперсия ошибки системы тем меньше, чем больше отличаются частотой спектральные плотности ошибок входных сигналов. Таким образом, задача комплексирования двух измерителей состоит в выборе такой частотной характеристики фильтра 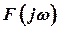 , чтобы после суммирования сигналов (см. рис. 2), параметр на выходе схемы
, чтобы после суммирования сигналов (см. рис. 2), параметр на выходе схемы 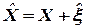 был близок к измеряемому параметру
был близок к измеряемому параметру 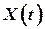 .
.
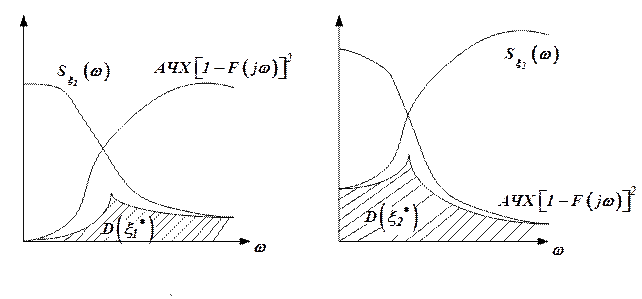 Рисунок 3
Рисунок 3
Схему компенсации можно реализовать, используя схему с обратной связью (рис. 4). Уравнение ошибок в этом случае эквивалентно полученным ранее для схемы компенсации без обратной связи (см. рис. 1).
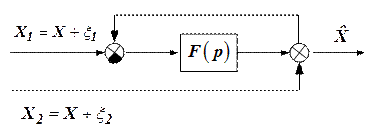
Рисунок 4
Для схемы компенсации, изображенной на рис. 4 можно записать:
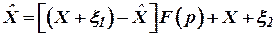 , ,
| (6) |
откуда имеем
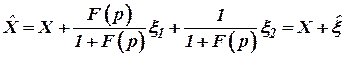 , ,
| (7) |
где
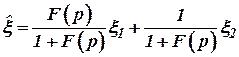 . .
| (8) |
Если 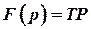 , то уравнение ошибок полностью совпадает.
, то уравнение ошибок полностью совпадает.
Пусть 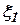 - низкочастотная помеха,
- низкочастотная помеха, 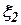 - высокочастотная помеха.
- высокочастотная помеха.
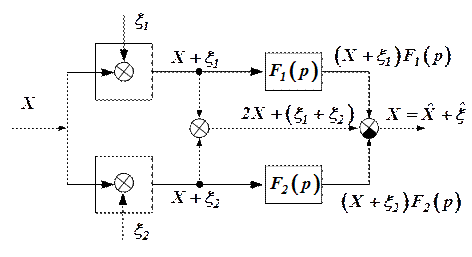
Низкочастотный фильтр - 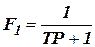 ;
;
Высокочастотный фильтр - 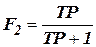 .
.
 =
= 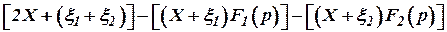 =
= 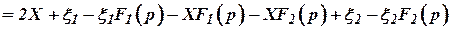 =
= 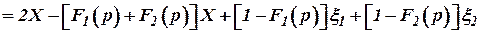 =
= 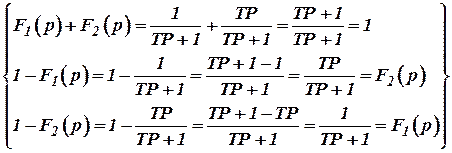 =
= 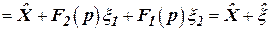 ,
,
где 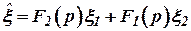 , то есть в данном случае динамические фильтры не пропускают соответственно на выход высокочастотную помеху
, то есть в данном случае динамические фильтры не пропускают соответственно на выход высокочастотную помеху 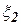 , то есть она не может пройти через низкочастотный динамический фильтр
, то есть она не может пройти через низкочастотный динамический фильтр 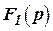 и наоборот фильтр
и наоборот фильтр 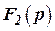 не пропускает низкочастотную составляющую помеху
не пропускает низкочастотную составляющую помеху 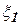 .
.
Дата добавления: 2015-08-14; просмотров: 937;
