Температурное поле в цилиндрической стенке при граничных условиях первого рода

Линейная плотность теплового потока.

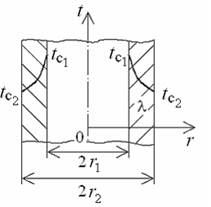
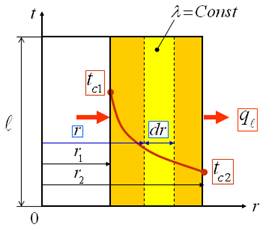
Рассмотрим стационарный процесс теплопроводности в бесконечной цилиндрической стенке (трубе) с внутренним диаметром d₁ и наружным диаметром d₂ (рис. 1) с постоянным коэффициентом теплопроводности λ. На наружных поверхностях трубы поддерживаются постоянными значения температуры t_c1 и t_c2. Необходимо найти распределение температуры в цилиндрической стенке и тепловой поток через нее.

Рис. 1

В рассматриваемом случае дифференциальное уравнение теплопроводности удобно записать в цилиндрической системе координат (ось Оz совмещена с осью трубы):

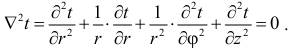(2)

Далее находим постоянную интегрирования С₂ и получим решение дифференциального уравнение теплопроводности (2):

,

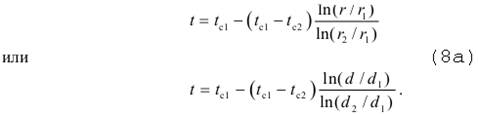
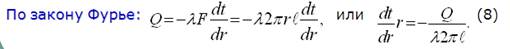Тогда с учетом (5) и (7) получим из уравнения (8)

Тепловой поток через единицу внутренней поверхности

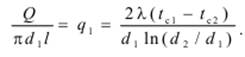
Тепловой поток через единицу внешней поверхности

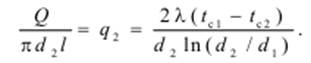
Тепловой поток через единицу длины трубы

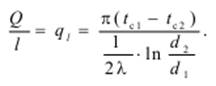(11)

Тепловой поток, отнесенный к единице длины трубы, имеет размерность Вт/м и называется линейной плотностью теплового потока q_l. Как видно из уравнения (9), при неизменном отношении диаметров линейная плотность теплового потока q_l не зависит от поверхности цилиндрической стенки.

Плотности теплового потока через внутреннюю и внешнюю стенки неодинаковы, причем первая больше второй.