Порядок вычисления выражений. Запись математических выражений
Выражения состоят из одной и долее следующих частей
– константы;
– переменные;
– знаки операций;
– элементы массива;
– функции.
Выражения используются для выполнения вычислений и сравнения значений, для предоставления переменных в качестве аргументов различным функциям и процедурам VBA. Все выражения Visual Basic вычисляются до значения, имеющего один из типов данных Visual Basic.
При вычислении сложных выражений VBA следует таким правилам:
– Части выражения, заключенные в круглые скобки, всегда вычисляются в первую очередь. Если выражение, заключенное в круглые скобки, является другим сложным выражением, VBA применяет эти же правила к выражению в круглых скобках;
– Конкретные операции выполняются в зависимости от иерархии операторов;
– Когда операторы имеют равный уровень приоритета, они вычисляются в порядке слева направо.
VBA вычисляет выражения в следующем порядке:
– Знаки арифметических операций.
– Знаки конкатенации (сложения) строк.
– Операторы сравнения.
– Логические операторы.
В таблице приведена иерархия операторов VBA. Операторы/операции перечислены в порядке от самого высокого приоритета до самого низкого. Операции, помещенные в одной и той же строке этой таблицы, имеют равный приоритет. Операции с равным приоритетом вычисляются слева направо так, как они появляются в выражении.
Иерархия операция от наивысшего до самого низкого приоритета показана в таблице 9.4
Таблица 9.4. Иерархия операторов/операций
| Оператор/ операция | Комментарии |
| ^ | Возведение в степень, наивысший приоритет |
| - | Унарный минус (присвоение знака числу) |
| *, / | Умножение и деление имеют равные приоритеты; они вычисляются по мере появления в выражении слева направо |
| \ | Вычисляет результат целочисленного деления первого математического выражения (X) на второе (Y). Перед вычислением значение каждого выражения округляется до целых по правилам математики. |
| Mod | Вычисляет остаток от деления первого математического выражения (X) на второе (Y). Перед делением значение каждого выражения округляется до целых по правилам математики |
| +, - | Сложение и вычитание имеют равный приоритет; они вычисляются по мере появления в выражении слева направо |
| & | Сложение строк выполняется после любых арифметических операций в выражении и перед любыми операциями сравнения или логическими операциями |
| <, <=, >, >=, =, <> | Все операторы сравнения имеют равные приоритеты и вычисляются по мере появления в выражении слева направо. Для группирования операторов сравнения в выражениях надо использовать круглые скобки |
| Not | Логическое отрицание |
| And | Функция И (логическое умножение) |
| Or | Функция ИЛИ (Логическое сложение) |
| Xor | Исключающее ИЛИ |
| Eqv | Функция эквивалентности |
| Imp | Функция импликации |
Математические выражения в программе записываются в одну строку. В строке должно быть не более 255 символов без учета пробелов. Главную роль в записи математических выражений играет правильное использование скобок. Они не только указывают очередность действий, но и отделяют аргументы математических функций, поэтому скобок бывает больше, чем других служебных знаков. Арифметическое выражение состоит из переменных, констант, функций и знаков арифметических действий.
Проверять длинные записи на предмет количества скобок становится легче, если знать правило: в любом выражении количество левых скобок должно быть равно количеству правых. Если равенства нет, то программа выдает сообщение об ошибке. Примеры записи некоторых арифметических выражений приведены в табл. 9.5.
Таблица 9.5
| Функция | Арифметическое выражение |
| PI = p | PI = 4*ATN(1) |
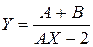 +3,15×1015 +3,15×1015 
| Y = (A+B)/(A*X-2)+3.15Е15 |
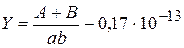
| Y = (А+В)/(А*В)-.17Е-13 |
| Y = SIN2X | Y = SIN(X)12 |
| Y = SIN X2 | Y = SIN(X*X) |
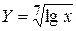
| Y = (LOG(X)/LOG(10))^(1/7) |
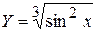
| Y = SIN(X)^(2/3) |
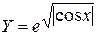
| Y = EXP(SQR(ABS(COS(X)))) |
| Y = ctg2x | Y = 1/TAN(X)^2 |
Y = arcsin 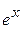
| Y = ATN(EXP(X)/SQR(1-EXP(2*X))) |
| Y = arccos3X | Y = ATN(SQR(1-9*X*X)/(3*X)) |
| Y = arccos3X | Y = 3.14/2-ATN(3*X/SQR(1-9*X*X)) |
Y = 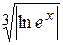
| Y = (ABS(LOG(EXP(X)))^(1/3) |
Y = 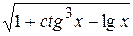
| Y = SQR(1+1/TAN(X)^3-LOG(X)/LOG(10)) |
| у = cos x2 | Y = COS (x ^ 2) |
| у = cos2 х | Y = COS (x) ^ 2 |
| y = cosa+bx | Y = COS (x) ^ (a + b) |
у = 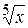
| Y = x ^ (1 / 5) |
у = 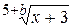
| У = (x + 3) ^ (1 / (5 + b)) |
y = 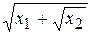
| Y = SQR(xl + SQR(x2)) |
y = 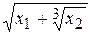
| Y = SQR(xl + x2 ^ (1 / 3)) |
z = 
| z = x ^ (y + 2) |
z = 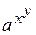
| z = a ^ (x ^ y) |
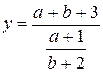
| y = (a +-b + 3)/((a. + l)/(b + 2)) |
| PI = p | PI = 4*ATN(1) |
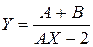 +3,15×1015 +3,15×1015 
| Y = (A+B)/(A*X-2)+3.15Е15 |
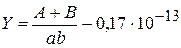
| Y = (А+В)/(А*В)-.17Е-13 |
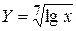
| Y = (LOG(X)/LOG(10))^(1/7) |
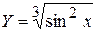
| Y = SIN(X)^(2/3) |
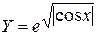
| Y = EXP(SQR(ABS(COS(X)))) |
| Y = ctg2x | Y = 1/TAN(X)^2 |
Y = arcsin 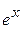
| Y = ATN(EXP(X)/SQR(1-EXP(2*X))) |
| Y = arccos3x | Y = ATN(SQR(1-9*X*X)/(3*X)) |
| Y = arccos3x | Y = 3.14/2-ATN(3*X/SQR(1-9*X*X)) |
Y = 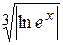
| Y = (ABS(LOG(EXP(X)))^(1/3) |
Y = 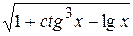
| Y = SQR(1+1/TAN(X)^3-LOG(X)/LOG(10)) |
Дата добавления: 2015-08-14; просмотров: 1623;
