Лекция 19. Рассмотрим два свойства амплитудно-фазовой характеристики цифровой системы:
Рассмотрим два свойства амплитудно-фазовой характеристики цифровой системы:
I. Амплитудно-фазовая характеристика цифровой системы представляет собой периодическую функцию относительной частоты 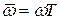 с периодом
с периодом 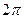 , т.е.
, т.е.
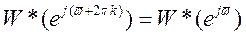 ,
, 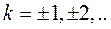 (55)
(55)
Действительно,
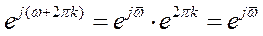 ,
,
так как
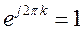 ,
, 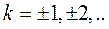
В связи с периодичностью 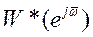 для полного суждения о ее поведении достаточно знать, какие значения она принимает при изменении
для полного суждения о ее поведении достаточно знать, какие значения она принимает при изменении 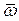 в любом диапазоне шириной
в любом диапазоне шириной 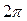 . Обычно используют диапазон низких частот
. Обычно используют диапазон низких частот 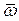 :от
:от 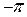 до
до 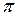 . Периодичность
. Периодичность 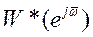 порождает так называемый стробоскопический эффект, который заключается в том, что цифровая система имеет одинаковую реакцию как на частоту
порождает так называемый стробоскопический эффект, который заключается в том, что цифровая система имеет одинаковую реакцию как на частоту 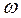 , так и на частоту
, так и на частоту 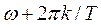 . Это обстоятельство еще раз свидетельствует о поглощении частот, вызванной дискретизацией.
. Это обстоятельство еще раз свидетельствует о поглощении частот, вызванной дискретизацией.
Годограф 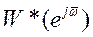 , построенный на комплексной плоскости
, построенный на комплексной плоскости 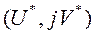 при изменении
при изменении 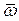 от -
от - 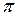 до
до 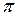 , называется диаграммой Найквиста. Кстати, относительная частота измеряется как [рад/выборку], где под выборкой понимается число периодов дискретизации Т, укладывающееся в период непрерывного сигнала
, называется диаграммой Найквиста. Кстати, относительная частота измеряется как [рад/выборку], где под выборкой понимается число периодов дискретизации Т, укладывающееся в период непрерывного сигнала 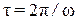 .
.
2. При изменении знака у частоты 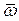 в аргументе амплитудно-фазовой характеристики получаем комплексно-сопряженное выражение, т. е.
в аргументе амплитудно-фазовой характеристики получаем комплексно-сопряженное выражение, т. е.
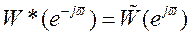 , (56)
, (56)
где 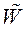 - символ комплексно-сопряженного выражения.
- символ комплексно-сопряженного выражения.
Действительно, представляя 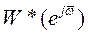 в алгебраической форме
в алгебраической форме
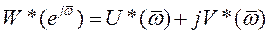 ,
,
где
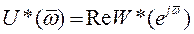 ,
, 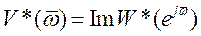 ,
,
и учитывая, что
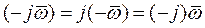 ,
,
находим
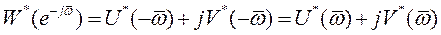 ,
,
откуда вытекает равенство (56). Таким образом, если известно выражение 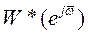 для положительных частот
для положительных частот 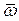 , то нетрудно найти значения этой характеристики и для отрицательных частот
, то нетрудно найти значения этой характеристики и для отрицательных частот 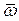 . Это свойство позволяет в два раза уменьшить диапазон изменения частоты
. Это свойство позволяет в два раза уменьшить диапазон изменения частоты 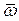 при исследовании поведения
при исследовании поведения 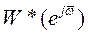 , т.е. вместо диапазона
, т.е. вместо диапазона 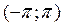 дает возможность ограничиться диапазоном
дает возможность ограничиться диапазоном 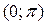 .
.
Амплитудно-фазовой характеристикой цифровой системы называется не только само выражение 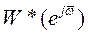 , но и годограф
, но и годограф 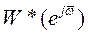 построенный, на комплексной плоскости
построенный, на комплексной плоскости 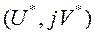 при изменении
при изменении 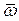 от 0 до
от 0 до  .
.
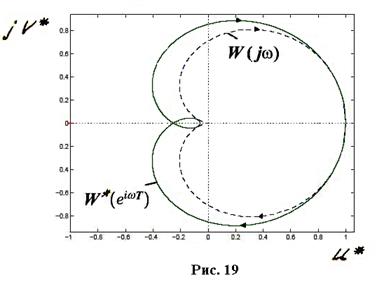
На рис. 19 представлены диаграммы Найквиста цифровой 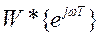 и соответствующей непрерывной
и соответствующей непрерывной 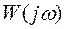 систем, причем диаграмма цифровой системы построена при изменении относительной частоты
систем, причем диаграмма цифровой системы построена при изменении относительной частоты 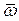 от
от 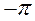 до
до  .
.
Дата добавления: 2015-08-14; просмотров: 714;
