Вычислительные алгоритмы метода возможных направлений

Метод возможных направлений осуществляется следующим образом.

1. Точка начального приближения находится в допустимой области .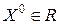

2. Последовательность точек 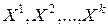, принадлежащих 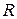, строится так, чтобы выполнялись неравенства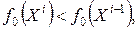 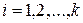. При этом, строя точку 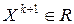так, чтобы выполнялось неравенство

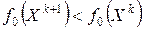, обнаруживаем, что либо 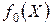не ограничена, либо такой точки не существует, т.е. 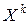- оптимальная точка. В обоих случаях процесс решения задачи прекращается. Задача решена.

Процедура построения точки 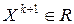состоит из двух этапов:

а) в точке 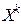определяется подходящее направление ,

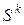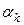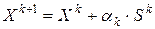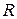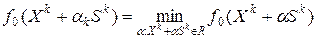б) определяется длина шага такая, что принадлежит и . Так как направление 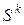подходящее, то при этом оказывается, что .

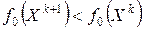3. Выбор подходящих направлений 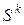в точках 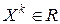производится так, что обеспечивается сходимость значений 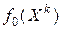к 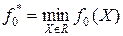, либо обнаруживается, что последовательность 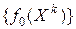не ограничена.

Методы возможных направлений можно рассматривать как градиентные методы с конечным шагом. Многие методы линейных и нелинейных задач математического программирования можно трактовать как методы возможных направлений. Они различаются лишь дополнительными требованиями к выбору начальной точки 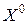, направления 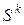и длины шага 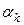. В частности к таким методам относится и симплекс- метод решения ЗЛП.