МЕТОД ВОЗМОЖНЫХ НАПРАВЛЕНИЙ
Рассмотрим задачу выпуклого программирования
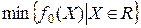 (13.1)
(13.1)
где допустимая область 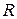 задается так
задается так
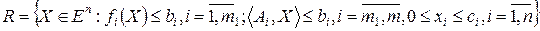 (13.2)
(13.2)
Поскольку функции 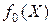 ,
, 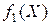 ,..,
,.., 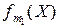 предполагаются выпуклыми, то в силу рассмотренных ранее свойств выпуклых функций задача (13.1)-(13.2) есть задача минимизации выпуклой функции на выпуклом множестве.
предполагаются выпуклыми, то в силу рассмотренных ранее свойств выпуклых функций задача (13.1)-(13.2) есть задача минимизации выпуклой функции на выпуклом множестве.
Введя в рассмотрение индексные множества
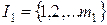 ,
, 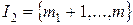 ,
, 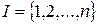
имеем
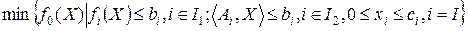 . (13.3)
. (13.3)
Для сокращения записей обозначим
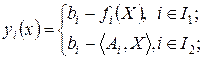
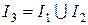 ,
,
Тогда ЗВП запишется в виде
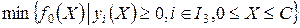 .
.
Идея метода возможных направлений (МВН) заключается в том, что в каждой очередной точке находится направление спуска такое, что перемещение точки по этому направлению на некоторое расстояние не приводит к нарушению ограничений задачи. Таким образом, МВН можно рассматривать как естественное распространение метода градиентного спуска на задачи минимизации с ограничениями. В отличие от других численных методов решения таких задач, метод возможных направлений обладает тем преимуществом, что для отыскания направления спуска достаточно решить задачу линейного программирования с небольшим числом ограничений.
Для описания метода возможных направлений введем ряд определений.
Определение 13.1.Направление, определяемое вектором 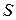 , называется возможным направлением в точке
, называется возможным направлением в точке 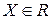 , если достаточно малое перемещение из
, если достаточно малое перемещение из 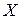 в направлении
в направлении 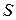 не выводит точку за пределы допустимой области, т.е., если существует такое число
не выводит точку за пределы допустимой области, т.е., если существует такое число 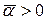 , что
, что 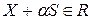 для всех
для всех 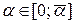 .
.
Очевидно, если 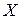 является внутренней точкой множества
является внутренней точкой множества 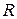 , то любое направление в этой точке является возможным.
, то любое направление в этой точке является возможным.
Определение 13.2. Возможное направление, определяемое вектором 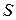 , называется подходящим направлением в точке
, называется подходящим направлением в точке 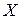 , если перемещение из точки
, если перемещение из точки 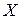 по этому направлению осуществляется с уменьшением значения функции, т.е., если
по этому направлению осуществляется с уменьшением значения функции, т.е., если 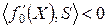 .
.
Очевиден геометрический смысл этого утверждения: угол между вектором, задающим подходящее направление в точке 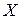 , и антиградиентом минимизируемой функции в данной точке острый.
, и антиградиентом минимизируемой функции в данной точке острый.
Следствием введенных определений является утверждение: если в точке 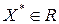 подходящих направлений нет, то функция
подходящих направлений нет, то функция 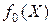 достигает в этой точке своего минимума на множестве
достигает в этой точке своего минимума на множестве 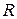 , т.е.
, т.е.
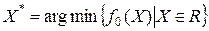 .
.
В самом деле. Пусть в точке 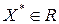 нет ни одного подходящего направления, т.е. для любого вектора
нет ни одного подходящего направления, т.е. для любого вектора 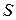 в точке
в точке 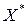 выполняется неравенство
выполняется неравенство 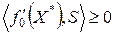 . Тогда при перемещении из точки
. Тогда при перемещении из точки 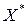 по любому из этих направлений функция
по любому из этих направлений функция 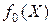 не убывает
не убывает
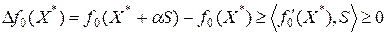 .
.
Следовательно, 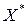 - точка локального минимума
- точка локального минимума 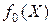 .
.
Дата добавления: 2015-08-14; просмотров: 805;
