Построение начального приближения

1. Строим точку , где С – заданный вектор.

2. Располагая точкой 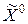, вычисляем значения функций

, .

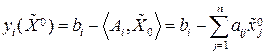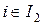Если значение функции 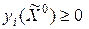, то точка 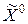удовлетворяет 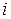-му линейному ограничению задачи, т.е. выполняется неравенство .

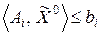Если число 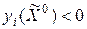, то в точке 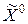не выполняется условие 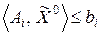и, следовательно, точка 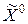не удовлетворяет 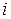-му линейному ограничению задачи.

3. Введем в рассмотрение неотрицательные числа 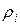, положив 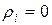для тех индексов 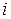, для которых 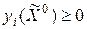и положив 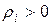для тех индексов, для которых .

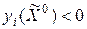4. Вводим дополнительную переменную 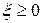, увеличивая тем самым размерность вектора неизвестных на единицу, и в (n+1)-мерном пространстве 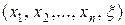формируем следующую задачу:

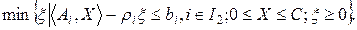
(13.4)

Таким образом, получим в (n+1)-мерном пространстве задачу минимизации линейной функции на множестве, задаваемом линейными ограничениями, т.е. задачу линейного программирования, которая решается за конечное число шагов симплекс-методом. При этом в качестве начального опорного плана можно выбрать точку

.

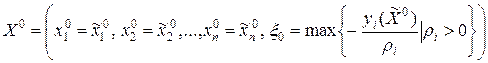В качестве 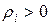можно взять .

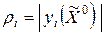Решая вспомогательную задачу (13.4) симплекс-методом, за конечное число шагов получим оптимальный план, в котором 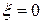. Тогда первые n компонент этого опорного плана определят точку 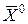, которая будет удовлетворять всем линейным ограничениям исходной задачи, т.е.

.

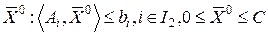5. Вычисляем 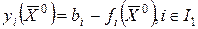. Задаем неотрицательные числа 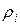и полагаем 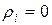для тех индексов 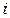, для которых 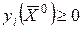и 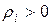для тех индексов, для которых .

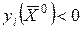6. Вводим дополнительную переменную 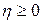и формулируем еще одну вспомогательную задачу, следующим образом:

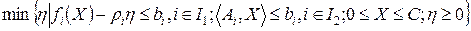(13.5)

Это есть задача выпуклого программирования, для которой известна начальная точка с координатами

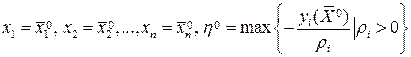
Если выбрать в качестве 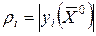, тогда начальная точка будет 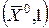. Очевидно, если в ходе решения ЗВП (13.5) на каком-то шаге получим 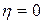, то есть вектор 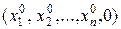, то соответствующий вектор 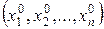определит искомую точку , которая будет являться начальной точкой исходной задачи.

Теорема 13.1. Если 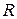непусто и регулярно по Слейтеру, то, применяя для решения задачи (13.5) метод возможных направлений, получим 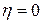за конечное число шагов.

Д о к а з а т е л ь с т в о. Допустим, что задача (13.5) решается методом возможных направлений без требования 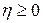. В силу условия Слейтера существует точка 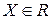такая, что 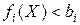для всех 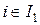, тогда ограничения 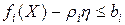, 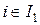допускают существование точки с компонентой 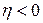. Так как 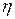минимизируется, то последовательность значений минимизируемой функции 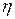будет сходиться к значению 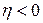. При этом, даже если оптимальное значение является пределом сходящейся последовательности, 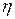становится неположительным за конечное число шагов. Следовательно, при условии 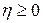оптимальное значение 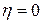достигается за конечное число шагов.

Замечание. Вместо того, чтобы последовательно удовлетворять сначала линейным, а затем нелинейным ограничениям, можно, избегая пунктов 5 и 6 и имея точку 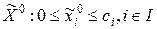, сразу решить задачу

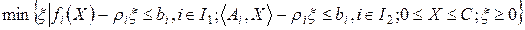(13.6)

где 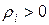для тех индексов 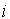, для которых .

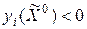Задача (13.6) является задачей выпуклого программирования, для которой за нулевое приближение можно взять точку

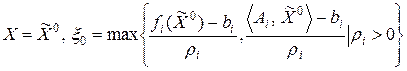
Однако, решение задачи (13.6) является более сложным, чем решение задач, которые рассматривались на шагах 5 и 6.