Диффузионная модель. Для этой же системы реакций при использовании диффузионной модели структуры потоков, модель реактора будет выглядеть следующим образом:

Для этой же системы реакций при использовании диффузионной модели структуры потоков, модель реактора будет выглядеть следующим образом:

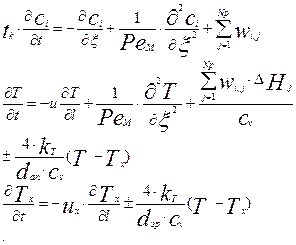(5.14)

Где Ре_М- критерий Пекле для описания переноса массы за счет обратного перемешивания, Ре_Т критерий Пекле для переноса тепла за счет обратного перемешивания. Практически эти критерии при существенном влиянии конвективных потоков будут одинаковы. Для движения теплоносителя в теплообменной рубашке используется обычно модель идеального вытеснения, так как в рубашке имеется обычно малое сечение и высокие скорости потока.

Источниковые и стоковые члены в уравнениях математической модели записываются на основании уравнений химической кинетики, рассмотренных нами в разделе «Кинетика». Таким образом, мы провели в соответствии со схемой разработки математических моделей, приведенной на рис. 2.1 структурный анализ процессов, происходящих в технологических объектах, получили описание отдельных процессов, а затем провели синтез модели на основании моделей отдельных блоков, составляющих сложный процесс. Таким же образом можно провести синтез моделей и на основе комбинированных моделей гидродинамки, рассмотренных нами в разделе «Структура потоков»

Например, для ячеечной модели, математическая модель с учетом кинетики, будет выглядеть следующим образом:

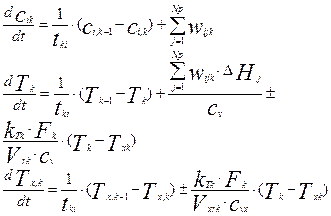(5.15)

Где k =1, 2…,К – номер реактора в каскаде.

Аналогичным образом можно получить математические модели с использованием модели структуры потока и системы кинетических уравнений для протекающих реакций.

Литература

1. В.А. Холоднов, Л.С. Кирьянова, Е.Н. Иванова и др.Математическое моделирование и методы реализации математических моделей, СПб.: «Руда и металлы», 2002. 170 с. Холоднов В.А.,
2. Дьяконов В.П., Иванова Е.Н., Кирьянова Л.С. Математическое моделирование и оптимизация химико-технологических процессов:Практическое руководство. — СПб.: АНО НПО «Профессионал», 2003. — 480.
3. Кафаров В.В. Методы кибернетики в химии и химической технологии. М: Химия, 1985. 448 с. .
4. Кафаров В.В., Мешалкин В.П. Анализ и синтез химико-технологических систем. М.: Химия, 1991.
5. В.К. Викторов, Н.В. Кузичкин, Г.Н. Вениаминова и др.Методы оптимизации химико-технологических систем: Учебное пособие / СПб.: Изд-во СПб ГТУ, 1999. 164 с.
6. Ахназарова С.Л., Кафаров В.В. Методы оптимизации эксперимента в химической технологии. М.: Высшая школа, 1985. 205 с.
7. Арис Р. Анализ процессов в химических реакторах. Л.: Химия, 1987. 327 с.
8. Артамонов А.Г., Володин В.М., Авдеев В.Г. Математическое моделирование и оптимизация плазмохимических процессов. М.: Химия, 1989.224 с.
9. Ю.В.Шариков, И.Н. Белоглазов, А.Ю. Фирсов Моделирование процессов и объектов в металлургии, СПбГГИ, Санкт-Петербург, 2006
10. Володин В.М., Бутусов О.Б., Добролюбов Г.В. Алгоритмизация и программирование инженерных задач средствами МАТКАДА: Учеб. пособие. М.: МГУ-ИЭ, 2000. 185 с.
11. Закгейм А.Ю. Введение в моделирование химико-технологических процессов. 2-е изд., перераб. и доп. М.: Химия, 1982. 288 с.