Поиск точки минимума по деформируемому многограннику

Практические трудности, возникающие при реализации поиска по правильному симплексу, такие как постоянство величины шага, отсутствие ускорения поиска и трудности при проведении поиска на искривленных поверхностях уровня, привели к необходимости некоторых улучшений метода. Рассмотрим метод поиска, в котором симплекс может изменять свою форму и уже не остается симплексом. Более подходящим для него оказалось название “деформируемый многогранник”.

В методе деформируемого многогранника, как и в предыдущем методе, функция 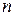независимых переменных минимизируется с использованием 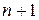вершин многогранника. Вершина, в которой значение функции 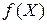максимально, проектируется через центр тяжести оставшихся вершин. Улучшенные значения функции 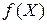находятся последовательной заменой точки с максимальным значением 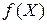на более “хорошие” точки, пока не будет найден минимум .

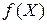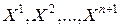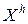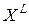Итак, пусть - вершины многогранника на некотором этапе поиска. Определим точки и , в которых функция имеет соответственно наибольшее и наименьшее значения:

.

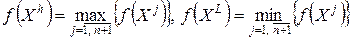Центр тяжести всех вершин, исключая 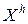, определим по формуле

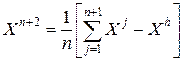
(5.1)

Процедура отыскания вершины, в которой 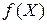имеет лучшее значение, состоит из четырех операций.

1) Отражение – проектирование точки 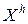через центр тяжести 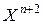в соответствии с соотношением

,

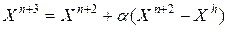(5.2)

где 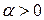– коэффициент отражения, 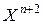- центр тяжести, вычисляемый по формуле (5.1).

2) Растяжение. Если 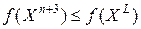, то вектор 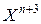- 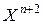растягивается в соответствии с соотношением

,

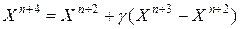(5.3)

где 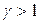–коэффициент растяжения. Если 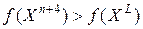, то вершина 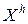заменяется на 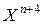и начинается новый этап поиска снова с операции отражения. В противном случае 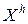заменяется на 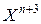и также осуществляется переход к операции отражения нового этапа.

3) Сжатие. Если 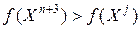, любого 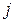: 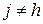, то вектор 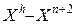сжимается в соответствии с формулой

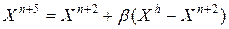
(5.4)

где 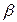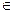(0;1)- коэффициент сжатия. Вершина 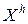заменяется на 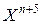и выполняется вновь операция отражения на новом этапе поиска.

4) Редукция. Если 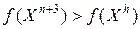, то все векторы 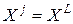уменьшаются, например, в 2 раза с отсчетом от 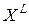в соответствии с формулой

, .

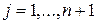(5.5)

Далее возвращаемся к операции отражения для продолжения поиска на новом этапе.

Критерий окончания поиска может быть выбран в виде условия

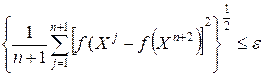
(5.6)

где 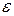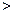0– достаточно малое число.

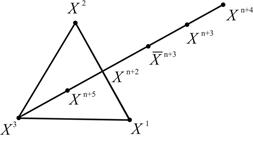
Геометрическая иллюстрация описанных процедур для пространства 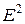приведена на рис. 5.2. и 5.3.

Рис. 5.2. Пробные точки 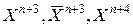, 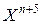для перехода к новому многограннику.

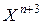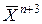Так как величина , то выбор точек и соответствует отражению; 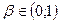, поэтому выбор точки 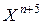соответствует сжатию, а 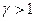и выбор точки 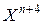приводит к растяжению симплекса.

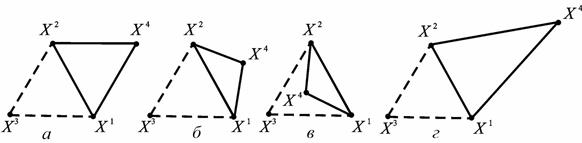
Рис.5.3. Новые многогранники, полученные в результате процедур отражения (а,б); сжатия (в); растяжения (г).

Деформируемый многогранник в отличие от жесткого симплекса адаптируется в процессе поиска к топографии целевой функции, вытягиваясь вдоль длинных наклонных плоскостей, изменяя направление в изогнутых впадинах и сжимаясь в окрестности минимума.