Задача. Дана плоскость (n,k) и одна проекция прямой m2.

Требуется найти недостающие проекции прямой m если известно, что она принадлежит плоскости, заданной пересекающимися прямыми n и k.

Проекция прямой m₂ пересекает прямые n и k в точках В₂ и С₂, для нахождения недостающих проекций прямой необходимо найти недостающие проекции точек В и С как точек лежащих на прямых соответственно n и k.

Таким образом точки В и С принадлежат плоскости заданной пересекающимися прямыми n и k, а прямая m проходит через эти точки, значит согласно аксиоме прямая принадлежит этой плоскости.

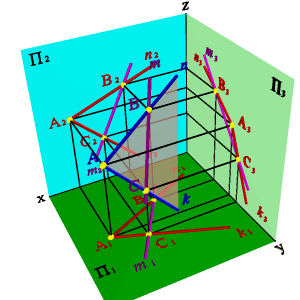
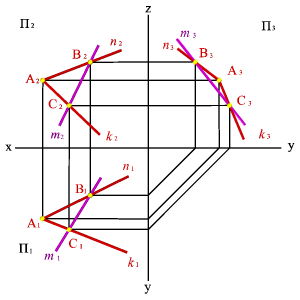
			а) модель		б) эпюр
Рисунок 5.14. Прямая и плоскость имеют две общие точки

Аксиома 2.Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой расположенной в этой плоскости (рис.5.15).