Условия параллельности и перпендикулярности

прямой и плоскости в пространстве.

Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.

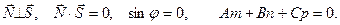
Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарны. Это условие выполняется, если векторное произведение этих векторов было равно нулю.

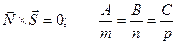
Поверхности второго порядка.

Определение. Поверхности второго порядка – это поверхности, уравнения которых в прямоугольной системе координат являются уравнениями второго порядка.

Цилиндрические поверхности.

Определение. Цилиндрическими поверхностями называются поверхности, образованные линиями, параллельными какой- либо фиксированной прямой.

Рассмотрим поверхности, в уравнении которых отсутствует составляющая z, т.е. направляющие параллельны оси Оz. Тип линии на плоскости ХOY (эта линия называется направляющей поверхности) определяет характер цилиндрической поверхности. Рассмотрим некоторые частные случаи в зависимости от уравнения направляющих:

1) 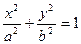- эллиптический цилиндр.

2) 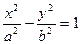- гиперболический цилиндр.

2) x² = 2py – параболический цилиндр.

Поверхности вращения.

Определение. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращенияс осью вращения d.

Если уравнение поверхности в прямоугольной системе координат имеет вид:

F(x² + y², z) = 0, то эта поверхность – поверхность вращения с осью вращения Оz.

Аналогично: F(x² + z², y) = 0 – поверхность вращения с осью вращения Оу,

F(z² + y², x) = 0 – поверхность вращения с осью вращения Ох.

Запишем уравнения поверхностей вращения для некоторых частных случаев:

1) - эллипсоид вращения

2) - однополостный гиперболоид вращения

3) 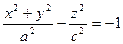- двуполостный гиперболоид вращения

4) 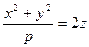- параболоид вращения

Аналогично могут быть записаны уравнения для рассмотренных выше поверхностей вращения, если осью вращения являются оси Ох или Оу.

Однако, перечисленные выше поверхности являются всего лишь частными случаями поверхностей второго порядка общего вида, некоторые типы которых рассмотрены ниже:

Сфера: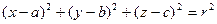

Трехосный эллипсоид: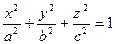

В сечении эллипсоида плоскостями, параллельными координатным плоскостям, получаются эллипсы с различными осями.

Однополостный гиперболоид:

Двуполостный гиперболоид:

Эллиптический параболоид:

Гиперболический параболоид:

Конус второго порядка: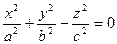

Квадратичные формы.

Определение: Однородный многочлен второй степени относительно переменных х₁ и х₂

Ф(х₁, х₂) = а₁₁ ,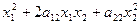

не содержащий свободного члена и неизвестных в первой степени, называется квадратичной формой переменных х₁ и х₂.

Определение: Однородный многочлен второй степени относительно переменных х₁, х₂ и х₃

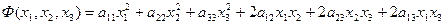
не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных х₁, х₂ и х₃.

Рассмотрим квадратичную форму двух переменных. Квадратичная форма имеет симметрическую матрицу А = . Определитель этой матрицы называется определителем квадратичной формы.

Пусть на плоскости задан ортогональный базис 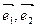. Каждая точка плоскости имеет в этом базисе координаты х₁, х₂.

Если задана квадратичная форма Ф(х₁, х₂) = а₁₁ 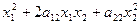, то ее можно рассматривать как функцию от переменных х₁ и х₂.