Уравнение прямой в пространстве по точке и

направляющему вектору.

Возьмем произвольную прямую и вектор 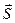(m, n, p), параллельный данной прямой. Вектор 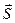называется направляющим вектором прямой.

На прямой возьмем две произвольные точки М₀(x₀, y₀, z₀) и M(x, y, z).

z

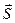M₁

M₀

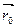
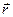
0 y

x

Обозначим радиус- векторы этих точек как 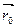и 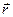, очевидно, что - = .

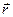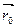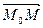Т.к. векторы 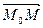и 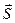коллинеарны, то верно соотношение 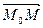= 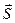t, где t – некоторый параметр.

Итого, можно записать: 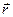= 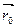+ 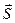t.

Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.

Это векторное уравнение может быть представлено в координатной форме:

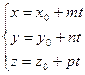
Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве:

.

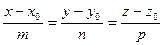Определение. Направляющими косинусамипрямой называются направляющие косинусы вектора 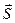, которые могут быть вычислены по формулам:

; .

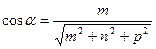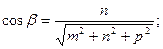
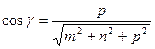Отсюда получим: m : n : p = cosa : cosb : cosg.

Числа m, n, p называются угловыми коэффициентами прямой. Т.к. 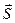- ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.